【题目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)当m=-1时,求A∪B;
(2)若AB,求实数m的取值范围;
(3)若A∩B=,求实数m的取值范围.
参考答案:
【答案】(1)A∪B={x|-2<x<3}(2)![]() (3)
(3)![]()
【解析】试题分析:(1)m=-1 ,用轴表示两个集合,做并集运算,注意空心点,实心点。(2)由于AB,首先要保证1-m>2m,即集合B非空,然后由数轴表示关系,注意等号是否可取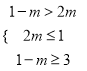 。(3)空集有两种情况,一种是集合B为空集,一种是集合B非空,此时用数灿表示,写出代数关系,注意等号是否可取。
。(3)空集有两种情况,一种是集合B为空集,一种是集合B非空,此时用数灿表示,写出代数关系,注意等号是否可取。
试题解析:(1)当m=-1时, B={x|-2<x<2},则A∪B={x|-2<x<3}
(2)由AB知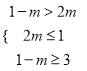 ,解得
,解得![]() ,
,
即m的取值范围是![]()
(3)由A∩B=得
①若![]() ,即
,即![]() 时,B=符合题意
时,B=符合题意
②若![]() ,即
,即![]() 时,需
时,需 或
或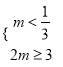
得![]() 或,即
或,即![]()
综上知![]() ,即实数的取值范围为
,即实数的取值范围为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信已成为人们常用的社交软件,“微信运动”是微信里由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的
 或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:步数
性别
0
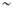 2000
20002001
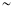 5000
50005001
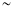 8000
80008001
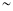 10000
10000>10000
男
1
2
4
7
6
女
0
3
9
6
2
若某人一天的走路步数超过8000步被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)利用样本估计总体的思想,试估计小明的所有微信好友中每日走路步数超过10000步的概率;
(2)根据题意完成下面的
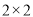 列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?积极型
懈怠型
总计
男
女
总计
附:
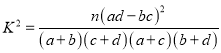
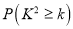
0.10
0.05
0.010
0.005
0.001
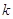
2.706
3.841
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB,☉O交直线OB于E,D两点,连接EC,CD.
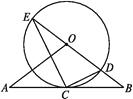
(1)求证:直线AB是☉O的切线;
(2)若tan∠CED=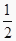 ,☉O的半径为3,求OA的长.
,☉O的半径为3,求OA的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校毕业典礼由6个节目组成,考虑整体效果,对节目演出顺序有如下要求:节目甲必须排在前三位,且节目丙、丁必须排在一起,则该校毕业典礼节目演出顺序的编排方案共有
A.
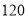 种 B.
种 B. 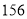 种 C.
种 C.  种 D.
种 D.  种
种 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
直角坐标系中曲线
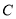 的参数方程
的参数方程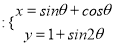 (
(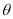 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, 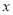 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, 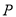 点的极坐标
点的极坐标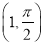 ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线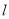 经过点
经过点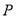 ,倾斜角为
,倾斜角为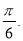
(1)写出曲线
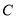 的直角坐标方程和直线
的直角坐标方程和直线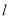 的参数方程;
的参数方程;(2)设直线
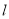 与曲线
与曲线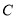 相交于
相交于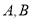 两点,求
两点,求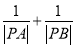 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.

(1)求∠BAE 的度数;
(2)求证:
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
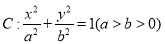 的离心率为
的离心率为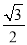 ,短轴长为2.
,短轴长为2.(1)求椭圆
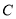 的标准方程;
的标准方程;(2)设直线
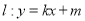 与椭圆
与椭圆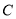 交于
交于 两点,
两点, 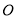 为坐标原点,若
为坐标原点,若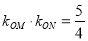 ,求原点
,求原点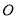 到直线
到直线 的距离的取值范围.
的距离的取值范围.
相关试题

