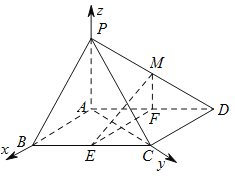
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() .
.
(Ⅲ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所在的角相等,求
所在的角相等,求![]() 的值.
的值.

参考答案:
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
试题分析:
(Ⅰ)由平行四边形的性质可得![]() ,有中点的性质有
,有中点的性质有![]() ,则
,则![]() ,
,
由面面垂直的性质定理可得![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() .
.
(Ⅱ)由三角形中位线的性质可得![]() ,则
,则![]() 平面
平面![]() ,同理,得
,同理,得![]() 平面
平面![]() ,利用面面平行的判断定理可得平面
,利用面面平行的判断定理可得平面![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() .
.
(Ⅲ)由题意可知![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴和
轴和![]() 轴建立空间直角坐标系,结合几何关系点的坐标可得平面
轴建立空间直角坐标系,结合几何关系点的坐标可得平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,由于直线
,由于直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,据此结合空间向量计算可得
所成的角相等,据此结合空间向量计算可得![]() .
.
试题解析:
(Ⅰ)证明:在平行四边形![]() 中,
中,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∵
,∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() ,∴
,∴![]() ,
,
∵侧面![]() 底面
底面![]() ,且
,且![]() ,
,
∴![]() 底面
底面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)证明:∵![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
∴![]() ,又∵
,又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,同理,得
,同理,得![]() 平面
平面![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,又∵
,又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅲ)解:∵![]() 底面
底面![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 两两垂直,故以
两两垂直,故以![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴和
轴和![]() 轴建立如图空间直角坐标系,
轴建立如图空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
易得平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则:
,则:
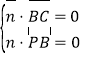 ,即
,即![]() ,令
,令![]() ,得
,得![]() ,
,
∴直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
∴![]() ,即
,即![]() ,
,
∴![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
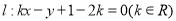 .
.(1)求证:无论
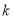 取何值,直线
取何值,直线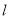 始终经过第一象限;
始终经过第一象限;(2)若直线
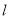 与
与 轴正半轴交于
轴正半轴交于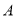 点,与
点,与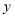 轴正半轴交于
轴正半轴交于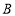 点,
点,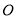 为坐标原点,设
为坐标原点,设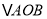 的面积为
的面积为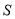 ,求
,求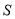 的最小值及此时直线
的最小值及此时直线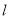 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 和四边形
和四边形 均是直角梯形,
均是直角梯形, ,二面角
,二面角 是直二面角,
是直二面角, ,
, ,
, .
.
(1)求证:
 面
面 ;
;(2)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(Ⅰ)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程.
处的切线方程.(Ⅱ)当
 时,若曲线
时,若曲线 上的点
上的点 都在不等式组
都在不等式组 所表示的平面区域内,试求
所表示的平面区域内,试求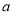 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校高一年级开设
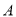 、
、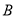 、
、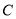 、
、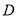 、
、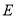 五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选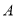 课程,不选
课程,不选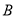 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.(Ⅰ)求甲同学选中
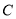 课程且乙同学未选中
课程且乙同学未选中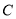 课程的概率.
课程的概率.(Ⅱ)用
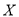 表示甲、乙、丙选中
表示甲、乙、丙选中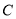 课程的人数之和,求
课程的人数之和,求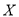 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬民族文化,某学校学生全员参与举行了“我爱国学,传诵经典”考试,并从中抽取
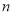 名学生的成绩(百分制)作为样本,得到频率分布直方图如图所示.成绩落在
名学生的成绩(百分制)作为样本,得到频率分布直方图如图所示.成绩落在 中的人数为20.
中的人数为20.
(1)求
 和
和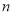 的值;
的值;(2)根据样本估计总体的思想,估计该校学生数学成绩的平均数
 和中位数
和中位数 ;(同一组数据中的数据以这组数据所在区间中点的值作代表)
;(同一组数据中的数据以这组数据所在区间中点的值作代表)(3)若成绩在80分以上(含80分)为“国学小达人”.若在样本中,利用分层抽样的方法从“国学小达人”中随机抽取5人,再从中抽取2人赠送一套国学经典,记“抽中的2名学生成绩都不低于90分”为事件
 ,求
,求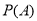 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图组合体中,三棱柱
 的侧面
的侧面 是圆柱的轴截面(过圆柱的轴,截圆柱所得的截面),
是圆柱的轴截面(过圆柱的轴,截圆柱所得的截面),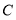 是圆柱底面圆周上不与
是圆柱底面圆周上不与 ,
, 重合的一个点.
重合的一个点.(1)求证:无论点
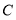 如何运动,平面
如何运动,平面
 平面
平面 ;
;(2)当点
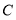 是弧
是弧 的中点时,求四棱锥
的中点时,求四棱锥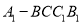 与圆柱的体积比.
与圆柱的体积比.
相关试题

