【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(Ⅱ)当![]() 时,若曲线
时,若曲线![]() 上的点
上的点![]() 都在不等式组
都在不等式组 所表示的平面区域内,试求
所表示的平面区域内,试求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:
(Ⅰ)根据导数的几何意义求出切线方程即可。(Ⅱ)将问题转化为:当![]() 时,不等式
时,不等式![]() 恒成立。构造函数设
恒成立。构造函数设![]() ,
, ![]() ,只需证明
,只需证明![]() 即可。因此将问题转化为求函数
即可。因此将问题转化为求函数![]() 在区间
在区间![]() 上的最大值和最小值即可。
上的最大值和最小值即可。
试题解析:
(Ⅰ) 当![]() 时,
时, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(Ⅱ)“当![]() 时,曲线
时,曲线![]() 上的点
上的点![]() 都在不等式组
都在不等式组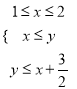 所表示的平面区域内,”
所表示的平面区域内,”
等价于“当![]() 时,
时, ![]() 恒成立。”
恒成立。”
设![]() ,
, ![]() ,
,
则![]() ,
,
①当![]() ,即
,即![]() 时,
时,
当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
故![]() ,
,
根据题意有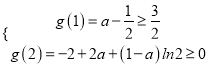 ,解得
,解得![]() .
.
②当![]() ,即
,即![]() 时,
时,
则当![]() ,
, ![]() ,
, ![]() 单调递增,
单调递增,
当![]() ,
, ![]() ,
, ![]() 单调递减.
单调递减.
∵![]() ,
,
∴![]() 不符合题意.
不符合题意.
③当![]() ,即
,即![]() 时,注意到
时,注意到![]() ,显然不合题意.
,显然不合题意.
综上所述,实数![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校高一年级开设
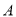 、
、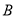 、
、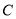 、
、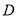 、
、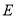 五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选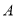 课程,不选
课程,不选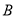 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.(Ⅰ)求甲同学选中
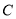 课程且乙同学未选中
课程且乙同学未选中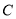 课程的概率.
课程的概率.(Ⅱ)用
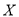 表示甲、乙、丙选中
表示甲、乙、丙选中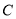 课程的人数之和,求
课程的人数之和,求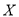 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
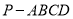 中,底面
中,底面 是平行四边形,
是平行四边形, 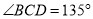 ,侧面
,侧面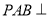 底面
底面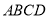 ,
, 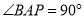 ,
,  ,
, 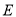 ,
, 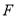 分别为
分别为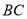 ,
, 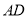 的中点,点
的中点,点 在线段
在线段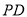 上.
上.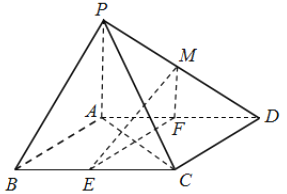
(1)求证:
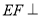 平面
平面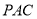 ;
;(2)如果直线
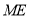 与平面
与平面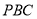 所成的角和直线
所成的角和直线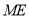 与平面
与平面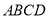 所成的角相等,求
所成的角相等,求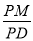 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知常数
 ,向量
,向量 ,
,  ,经过点
,经过点 ,以
,以 为方向向量的直线与经过点
为方向向量的直线与经过点 ,以
,以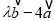 为方向向量的直线交于点
为方向向量的直线交于点 ,其中
,其中 .
.(
 )求点
)求点 的轨迹方程,并指出轨迹
的轨迹方程,并指出轨迹 .
.(
 )若点
)若点 ,当
,当 时,
时,  为轨迹
为轨迹 上任意一点,求
上任意一点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为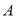 ,离心离为
,离心离为 ,点
,点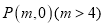 满足条件
满足条件 .
.(Ⅰ)求
 的值.
的值.(Ⅱ)设过点
 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,记
两点,记 和
和 的面积分别为
的面积分别为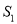 、
、 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是直角梯形,
是直角梯形,  ,又
,又 ,直线
,直线 与直线
与直线 所成的角为
所成的角为 .
.
(1)求证:
 ;
;(2)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知中心在原点,焦点在
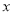 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为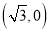 ,
, 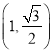 是椭圆上的一个点.
是椭圆上的一个点.(1)求椭圆的标准方程;
(2)设椭圆的上、下顶点分别为
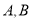 ,
, 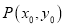 (
(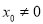 )是椭圆上异于
)是椭圆上异于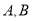 的任意一点,
的任意一点, 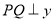 轴,
轴, 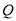 为垂足,
为垂足, 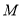 为线段
为线段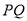 中点,直线
中点,直线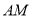 交直线
交直线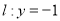 于点
于点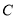 ,
, 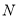 为线段
为线段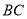 的中点,如果
的中点,如果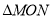 的面积为
的面积为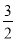 ,求
,求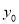 的值.
的值.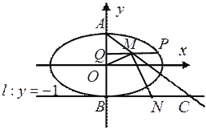
相关试题

