【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(![]() )
)![]() ,
,![]() ;(
;(![]() )证明见解析;(
)证明见解析;(![]() 证明见解析.
证明见解析.
【解析】
(![]() )由
)由![]() ,解得
,解得![]() ,
,![]() ;由
;由![]() ,解得
,解得![]() ,,
,,![]() ;(
;(![]() )若
)若![]() ,则
,则![]() 成立;若
成立;若![]() ,设
,设![]() 为
为![]() 中任意一个元素,则有
中任意一个元素,则有![]() ,可得
,可得![]() ,故
,故![]() ,从而可得结果;(
,从而可得结果;(![]() )①当
)①当![]() 时,
时,![]() 的图象在
的图象在![]() 轴的上方,可得对于
轴的上方,可得对于![]() ,
,![]() 恒成立,则
恒成立,则![]() .②当
.②当![]() 时,
时,![]() 的图象在
的图象在![]() 轴的下方,可得对于任意
轴的下方,可得对于任意![]() ,
,![]() 恒成立,则
恒成立,则![]() .
.
(![]() )由
)由![]() ,
,
得![]() ,
,
解得![]() ,
,
由![]() ,得
,得![]() ,
,
解得![]() ,
,
∴![]() ,
,![]() .
.
(![]() )若
)若![]() ,
,
则![]() 成立,
成立,
若![]() ,
,
设![]() 为
为![]() 中任意一个元素,
中任意一个元素,
则有![]() ,
,
∴![]() ,
,
故![]() ,
,
∴![]() .
.
(![]() )由
)由![]() ,得方程
,得方程![]() 无实数解,
无实数解,
∴![]() .
.
①当![]() 时,
时,![]() 的图象在
的图象在![]() 轴的上方,
轴的上方,
所以任意![]() ,
,![]() 恒成立,
恒成立,
即对于任意![]() ,
,![]() 恒成立,
恒成立,
对于![]() ,则有
,则有![]() 成立,
成立,
∴对于![]() ,
,![]() 恒成立,
恒成立,
则![]() .
.
②当![]() 时,
时,![]() 的图象在
的图象在![]() 轴的下方,
轴的下方,
所以任意![]() ,
,![]() 恒成立,
恒成立,
即对于![]() ,
,![]() 恒成立,
恒成立,
对于实数![]() ,则有
,则有![]() 成立,
成立,
所以对于任意![]() ,
,![]() 恒成立,
恒成立,
则![]() ,
,
综上知,对于![]() ,
,
当![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
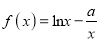 ,a为常数
,a为常数(1)判断f(x)在定义域内的单调性
(2)若f(x)在
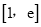 上的最小值为
上的最小值为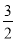 ,求a的值
,求a的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,经过点
中,经过点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 和
和 .
.(1)求
 的取值范围;
的取值范围;(2)设椭圆与
 轴正半轴、
轴正半轴、 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在常数
,是否存在常数 ,使得向量
,使得向量 与
与 共线?如果存在,求
共线?如果存在,求 值;如果不存在,请说明理由.
值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知矩形
 的长为2,宽为1,
的长为2,宽为1, .
. 边分别在
边分别在 轴.
轴. 轴的正半轴上,
轴的正半轴上, 点与坐标原点重合(如图所示)。将矩形折叠,使
点与坐标原点重合(如图所示)。将矩形折叠,使 点落在线段
点落在线段 上。
上。
(1)若折痕所在直线的斜率为
 ,试求折痕所在直线的方程;
,试求折痕所在直线的方程;(2)当
 时,求折痕长的最大值;
时,求折痕长的最大值; (3)当
 时,折痕为线段
时,折痕为线段 ,设
,设 ,试求
,试求 的最大值。
的最大值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设离心率为
 的椭圆E:
的椭圆E:  +
+  =1(a>b>0)的左、右焦点为F1 , F2 , 点P是E上一点,PF1⊥PF2 , △PF1F2内切圆的半径为
=1(a>b>0)的左、右焦点为F1 , F2 , 点P是E上一点,PF1⊥PF2 , △PF1F2内切圆的半径为 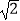 ﹣1.
﹣1.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线y=x+2,A、B在椭圆E上,若矩形ABCD的周长为 ,求直线AB的方程.
,求直线AB的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ex+ax2(a∈R).
(1)若函数f(x)在R上单调,且y=f′(x)有零点,求a的值;
(2)若对x∈[0,+∞),有 ≥1,求a的取值范围.
≥1,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校有两个参加国际中学生交流活动的代表名额,为此该学校高中部推荐2男1女三名候选人,初中部也推荐了1男2女三名候选人。若从6名学生中人选2人做代表。
求:(1)选出的2名同学来自不同年相级部且性别同的概率;
(2)选出的2名同学都来自高中部或都来自初中部的概率。
相关试题

