【题目】设函数f(x)=ex+ax2(a∈R).
(1)若函数f(x)在R上单调,且y=f′(x)有零点,求a的值;
(2)若对x∈[0,+∞),有 ![]() ≥1,求a的取值范围.
≥1,求a的取值范围.
参考答案:
【答案】
(1)解:f′(x)=ex+2ax,
记g(x)=ex+2ax,则g′(x)=ex+2a,
①a=0时,f(x)=ex,显然不合题意;
②a>0时,g′(x)>0,f′(x)在R递增,
∵f′(0)=1>0,f′(﹣ ![]() )<0,
)<0,
故y=f′(x)有唯一零点x1,显然x∈(﹣∞,x1)时,f′(x)<0,
x∈(x1,+∞)时,f′(x)>0,f(x)在R不单调,不合题意;
③a<0时,由g′(x)=0得x=ln(﹣2a),于是f′(x)在(﹣∞,ln(﹣2a))递减,
在(ln(﹣2a),+∞)递增,因此要满足条件,必须且只需f′[ln(﹣2a)]=0,
即﹣2a+2aln(﹣2a)=0,解得:a=﹣ ![]()
(2)解:a<0时,若x>﹣ ![]() ,则ax+1<0,根据指数函数和幂函数的增长速度知:
,则ax+1<0,根据指数函数和幂函数的增长速度知:
存在x0,当x>x0时,必有ex>﹣ax2,即ex+ax2>0,
因此x>max{﹣ ![]() ,x0},有
,x0},有 ![]() <0,显然不合题意,
<0,显然不合题意,
当a≥0时,记h(x)=ex+ax2﹣ax﹣1,则 ![]() ≥1当且仅当h(x)≥0,
≥1当且仅当h(x)≥0,
h′(x)=ex+2ax﹣a,显然h′(x)在[0,+∞)递增,
①a≤1时,由h′(0)=1﹣a<1,h′(1)=e+a>0,
得h′(x)=0在[0,+∞)上有且只有1个实数根,
不妨设该实根为x1,当0<x<x1时,h′(x)<0,从而h(x)在(0,x1)递减,
故x∈(0,x1)时,h(x)<h(0)=0,不合题意,
综上,a的范围是[0,1]
【解析】(1)求出函数的导数,通过讨论a的范围结合函数的单调性以及函数的零点求出a的值即可;(2)通过讨论a的范围,根据函数的单调性求出函数的最值,从而确定满足条件的a的范围即可.
【考点精析】掌握利用导数研究函数的单调性和函数的最大(小)值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知矩形
 的长为2,宽为1,
的长为2,宽为1, .
. 边分别在
边分别在 轴.
轴. 轴的正半轴上,
轴的正半轴上, 点与坐标原点重合(如图所示)。将矩形折叠,使
点与坐标原点重合(如图所示)。将矩形折叠,使 点落在线段
点落在线段 上。
上。
(1)若折痕所在直线的斜率为
 ,试求折痕所在直线的方程;
,试求折痕所在直线的方程;(2)当
 时,求折痕长的最大值;
时,求折痕长的最大值; (3)当
 时,折痕为线段
时,折痕为线段 ,设
,设 ,试求
,试求 的最大值。
的最大值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,若
,若 ,则称
,则称 为
为 的“不动点”;若
的“不动点”;若 ,则称
,则称 为
为 的“稳定点”.函数
的“稳定点”.函数 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为 和
和 ,即
,即 ,
, .
.(
 )设函数
)设函数 ,求集合
,求集合 和
和 .
.(
 )求证:
)求证: .
.(
 )设函数
)设函数 ,且
,且 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设离心率为
 的椭圆E:
的椭圆E:  +
+  =1(a>b>0)的左、右焦点为F1 , F2 , 点P是E上一点,PF1⊥PF2 , △PF1F2内切圆的半径为
=1(a>b>0)的左、右焦点为F1 , F2 , 点P是E上一点,PF1⊥PF2 , △PF1F2内切圆的半径为 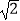 ﹣1.
﹣1.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线y=x+2,A、B在椭圆E上,若矩形ABCD的周长为 ,求直线AB的方程.
,求直线AB的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校有两个参加国际中学生交流活动的代表名额,为此该学校高中部推荐2男1女三名候选人,初中部也推荐了1男2女三名候选人。若从6名学生中人选2人做代表。
求:(1)选出的2名同学来自不同年相级部且性别同的概率;
(2)选出的2名同学都来自高中部或都来自初中部的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】 在平行四边形ABCD中,A(1,1),
 =(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若 =(3,5),求点C的坐标;(2) 当|
=(3,5),求点C的坐标;(2) 当| |=|
|=| |时,求点P的轨迹.
|时,求点P的轨迹. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线 交此抛物线于不同的两个点
交此抛物线于不同的两个点 、
、 .
.(
 )当直线
)当直线 过点
过点 时,证明
时,证明 ,
, 为定值.
为定值.(
 )当
)当 时,直线
时,直线 是否过定点?若过定点,求出定点坐标;反之,请说明理由.
是否过定点?若过定点,求出定点坐标;反之,请说明理由.(
 )记
)记 ,如果直线
,如果直线 过点
过点 ,设线段
,设线段 的中点为
的中点为 ,线段
,线段 的中点为
的中点为 .问是否存在一条直线和一个定点,使得点
.问是否存在一条直线和一个定点,使得点 到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
相关试题

