【题目】在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1,![]() .
.![]() 边分别在
边分别在![]() 轴.
轴.![]() 轴的正半轴上,
轴的正半轴上,![]() 点与坐标原点重合(如图所示)。将矩形折叠,使
点与坐标原点重合(如图所示)。将矩形折叠,使![]() 点落在线段
点落在线段![]() 上。
上。

(1)若折痕所在直线的斜率为![]() ,试求折痕所在直线的方程;
,试求折痕所在直线的方程;
(2)当![]() 时,求折痕长的最大值;
时,求折痕长的最大值;
(3)当![]() 时,折痕为线段
时,折痕为线段![]() ,设
,设![]() ,试求
,试求![]() 的最大值。
的最大值。
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)对k=0,![]() 分类讨论,将矩形折叠后
分类讨论,将矩形折叠后![]() 点落在线段
点落在线段![]() 上的点记为
上的点记为![]() ,先求G的坐标,再求折痕所在的直线与
,先求G的坐标,再求折痕所在的直线与![]() 的交点坐标,写出直线的点斜式方程.(2) 先求出折痕直线交
的交点坐标,写出直线的点斜式方程.(2) 先求出折痕直线交![]() 于点
于点![]() ,交
,交![]() 轴于
轴于![]() ,再求
,再求![]() 的最大值,即得折痕长的最大值.(3)先求得
的最大值,即得折痕长的最大值.(3)先求得![]() ,再求t的表达式和其最大值.
,再求t的表达式和其最大值.
(1) ①当![]() 时,此时
时,此时![]() 点与
点与![]() 点重合, 折痕所在的直线方程
点重合, 折痕所在的直线方程![]()
②当![]() 时,将矩形折叠后
时,将矩形折叠后![]() 点落在线段
点落在线段![]() 上的点记为
上的点记为![]() ,
,
所以![]() 与
与![]() 关于折痕所在的直线对称,
关于折痕所在的直线对称,
有![]()
![]()
![]()
![]()
![]()
故![]() 点坐标为
点坐标为![]() ,
,
从而折痕所在的直线与![]() 的交点坐标(线段
的交点坐标(线段![]() 的中点)为
的中点)为![]()
折痕所在的直线方程![]() ,即
,即![]()
由①②得折痕所在的直线方程为:![]()
(2)当![]() 时,折痕的长为2;
时,折痕的长为2;
当![]() 时,折痕直线交
时,折痕直线交![]() 于点
于点![]() ,交
,交![]() 轴于
轴于![]()
∵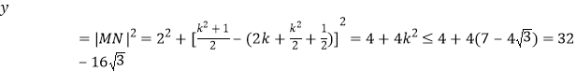
∴折痕长度的最大值为![]() 。
。
而![]() ,故折痕长度的最大值为
,故折痕长度的最大值为![]()
(3)当![]() 时,折痕直线交
时,折痕直线交![]() 于
于![]() ,交
,交![]() 轴于
轴于![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() (当且仅当
(当且仅当![]() 时取“=”号)
时取“=”号)
∴当![]() 时,
时,![]() 取最大值,
取最大值,![]() 的最大值是
的最大值是![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某学校高三年级共
 名男生中随机抽取
名男生中随机抽取 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于 和
和 之间,将测量结果按如下方式分成八组,第一组
之间,将测量结果按如下方式分成八组,第一组 ;第二组
;第二组 ,
, ,第八组
,第八组 ,如图是按上述分组方法得到的频率分布直方图的一部分,若第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,如图是按上述分组方法得到的频率分布直方图的一部分,若第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(
 )估计这所学校高三年级全体男生身高
)估计这所学校高三年级全体男生身高 以上(含
以上(含 )的人数.
)的人数.(
 )求第六组、第七组的频率并补充完整频率分布直方图.(铅笔作图并用中性笔描黑).
)求第六组、第七组的频率并补充完整频率分布直方图.(铅笔作图并用中性笔描黑).(
 )若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为
)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 、
、 ,求满足
,求满足 的事件概率.
的事件概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
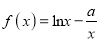 ,a为常数
,a为常数(1)判断f(x)在定义域内的单调性
(2)若f(x)在
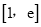 上的最小值为
上的最小值为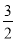 ,求a的值
,求a的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,经过点
中,经过点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 和
和 .
.(1)求
 的取值范围;
的取值范围;(2)设椭圆与
 轴正半轴、
轴正半轴、 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在常数
,是否存在常数 ,使得向量
,使得向量 与
与 共线?如果存在,求
共线?如果存在,求 值;如果不存在,请说明理由.
值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,若
,若 ,则称
,则称 为
为 的“不动点”;若
的“不动点”;若 ,则称
,则称 为
为 的“稳定点”.函数
的“稳定点”.函数 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为 和
和 ,即
,即 ,
, .
.(
 )设函数
)设函数 ,求集合
,求集合 和
和 .
.(
 )求证:
)求证: .
.(
 )设函数
)设函数 ,且
,且 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设离心率为
 的椭圆E:
的椭圆E:  +
+  =1(a>b>0)的左、右焦点为F1 , F2 , 点P是E上一点,PF1⊥PF2 , △PF1F2内切圆的半径为
=1(a>b>0)的左、右焦点为F1 , F2 , 点P是E上一点,PF1⊥PF2 , △PF1F2内切圆的半径为 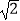 ﹣1.
﹣1.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线y=x+2,A、B在椭圆E上,若矩形ABCD的周长为 ,求直线AB的方程.
,求直线AB的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ex+ax2(a∈R).
(1)若函数f(x)在R上单调,且y=f′(x)有零点,求a的值;
(2)若对x∈[0,+∞),有 ≥1,求a的取值范围.
≥1,求a的取值范围.
相关试题

