【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)没有
(2)没有
【解析】解:(1)由已知条件知直线l的方程为
y=kx+![]() ,
,
代入椭圆方程得![]() +(kx+
+(kx+![]() )2=1.
)2=1.
整理得![]() x2+2
x2+2![]() kx+1=0.①
kx+1=0.①
直线l与椭圆有两个不同的交点P和Q等价于Δ=8k2-4![]() =4k2-2>0,
=4k2-2>0,
解得k<-![]() 或k>
或k>![]() ,
,
即k的取值范围为![]() ∪
∪![]() .
.
(2)设P(x1,y1),Q(x2,y2),
则![]() +
+![]() =(x1+x2,y1+y2),
=(x1+x2,y1+y2),
由方程①得x1+x2=-![]() .②
.②
又y1+y2=k(x1+x2)+2![]() =
=![]() ,③
,③
而A(![]() ,0),B(0,1),
,0),B(0,1),![]() =(-
=(-![]() ,1),
,1),
所以![]() +
+![]() 与
与![]() 共线等价于x1+x2=-
共线等价于x1+x2=-![]() (y1+y2).
(y1+y2).
将②③代入上式,解得k=![]() .
.
由(1)知k<-![]() 或k>
或k>![]() ,故没有符合题意的常数k.
,故没有符合题意的常数k.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,四边形
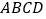 中,
中,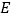 是
是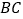 的中点,
的中点, 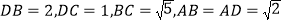 .将(图甲)沿直线
.将(图甲)沿直线 折起,使二面角
折起,使二面角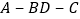 为
为 (如图乙).
(如图乙). (1)求证:
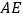 ⊥平面
⊥平面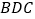
(2)求点
 到平面
到平面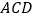 的距离.
的距离.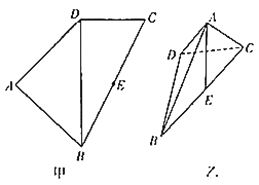
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面为正方形的四棱锥P-ABCD中,侧棱PD⊥底面ABCD,PD=DC,点E是线段PC的中点.

(1)求异面直线AP与BE所成角的大小;
(2)若点F在线段PB上,使得二面角F-DE-B的正弦值为
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若f(x)=ex+ae﹣x为偶函数,则f(x﹣1)<
 的解集为( )
的解集为( )
A.(2,+∞)
B.(0,2)
C.(﹣∞,2)
D.(﹣∞,0)∪(2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数
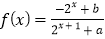 是奇函数.
是奇函数.(1)求a,b的值;
(2)解关于t的不等式f(t2-2t)+f(2t2-1)<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为某几何体形状的纸盒的三视图,在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,则小正四面体的棱长的最大值为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)试讨论函数
 的单调性;
的单调性;(2)证明:
 .
.
相关试题

