【题目】己知n为正整数,数列{an}满足an>0,4(n+1)an2﹣nan+12=0,设数列{bn}满足bn= ![]()
(1)求证:数列{ ![]() }为等比数列;
}为等比数列;
(2)若数列{bn}是等差数列,求实数t的值:
(3)若数列{bn}是等差数列,前n项和为Sn , 对任意的n∈N* , 均存在m∈N* , 使得8a12Sn﹣a14n2=16bm成立,求满足条件的所有整数a1的值.
参考答案:
【答案】
(1)证明:数列{an}满足an>0,4(n+1)an2﹣nan+12=0,
∴ ![]() =
= ![]() an+1,即
an+1,即 ![]() =2
=2 ![]() ,
,
∴数列{ ![]() }是以a1为首项,以2为公比的等比数列
}是以a1为首项,以2为公比的等比数列
(2)解:由(1)可得: ![]() =
= ![]() ,∴
,∴ ![]() =n
=n ![]() 4n﹣1.
4n﹣1.
∵bn= ![]() ,∴b1=
,∴b1= ![]() ,b2=
,b2= ![]() ,b3=
,b3= ![]() ,
,
∵数列{bn}是等差数列,∴2× ![]() =
= ![]() +
+ ![]() ,
,
∴ ![]() =
= ![]() +
+ ![]() ,
,
化为:16t=t2+48,解得t=12或4
(3)解:数列{bn}是等差数列,由(2)可得:t=12或4.
①t=12时,bn= ![]() =
= ![]() ,Sn=
,Sn=  ,
,
∵对任意的n∈N*,均存在m∈N*,使得8a12Sn﹣a14n2=16bm成立,
∴8 ![]() ×
×  ﹣a14n2=16×
﹣a14n2=16× ![]() ,
,
∴ ![]()
![]() =
= ![]() ,n=1时,化为:﹣
,n=1时,化为:﹣ ![]() =
= ![]() >0,无解,舍去.
>0,无解,舍去.
②t=4时,bn= ![]() =
= ![]() ,Sn=
,Sn=  ,
,
对任意的n∈N*,均存在m∈N*,使得8a12Sn﹣a14n2=16bm成立,
∴8 ![]() ×
×  ﹣a14n2=16×
﹣a14n2=16× ![]() ,
,
∴n ![]() =4m,
=4m,
∴a1=2 ![]() .∵a1为正整数,∴
.∵a1为正整数,∴ ![]() =
= ![]() k,k∈N*.
k,k∈N*.
∴满足条件的所有整数a1的值为{a1|a1=2 ![]() ,n∈N*,m∈N*,且
,n∈N*,m∈N*,且 ![]() =
= ![]() k,k∈N*}
k,k∈N*}
【解析】(1)数列{an}满足an>0,4(n+1)an2﹣nan+12=0,化为: ![]() =2×
=2× ![]() ,即可证明.(2)由(1)可得:
,即可证明.(2)由(1)可得: ![]() =
= ![]() ,可得
,可得 ![]() =n
=n ![]() 4n﹣1 . 数列{bn}满足bn=
4n﹣1 . 数列{bn}满足bn= ![]() ,可得b1 , b2 , b3 , 利用数列{bn}是等差数列即可得出t.(3)根据(2)的结果分情况讨论t的值,化简8a12Sn﹣a14n2=16bm , 即可得出a1 .
,可得b1 , b2 , b3 , 利用数列{bn}是等差数列即可得出t.(3)根据(2)的结果分情况讨论t的值,化简8a12Sn﹣a14n2=16bm , 即可得出a1 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,
 .
.
(1)证明: A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的首项
的首项 ,前
,前 项和为
项和为 ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前n项和Tn,并证明:1≤Tn<
的前n项和Tn,并证明:1≤Tn< .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
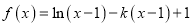 .
.(1)求函数
 的单调区间;
的单调区间;(2)若
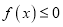 恒成立,试确定实数
恒成立,试确定实数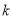 的取值范围;
的取值范围;(3)证明:
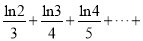
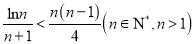 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是抛物线
是抛物线 :
:  (
( )上一点,
)上一点,  是抛物线的焦点,
是抛物线的焦点,  且
且 .
.(1)求抛物线
 的方程;
的方程;(2)已知
 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 、
、 两点,以
两点,以 为圆心的圆
为圆心的圆 与直线
与直线 相切,试判断圆
相切,试判断圆 与直线
与直线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
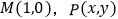 为平面上一动点,
为平面上一动点,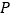 到直线
到直线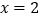 的距离为
的距离为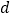 ,
,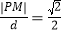 .
.(Ⅰ)求点
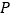 的轨迹
的轨迹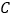 的方程;
的方程;(Ⅱ)不过原点
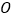 的直线
的直线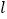 与
与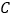 交于
交于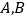 两点,线段
两点,线段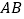 的中点为
的中点为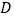 ,直线
,直线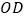 与直线
与直线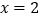 交点的纵坐标为1,求
交点的纵坐标为1,求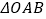 面积的最大值及此时直线
面积的最大值及此时直线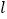 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是抛物线
是抛物线 :
:  (
( )上一点,
)上一点,  是抛物线的焦点,
是抛物线的焦点,  且
且 .
.(1)求抛物线
 的方程;
的方程;(2)已知
 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 、
、 两点,以
两点,以 为圆心的圆
为圆心的圆 与直线
与直线 相切,试判断圆
相切,试判断圆 与直线
与直线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
相关试题

