【题目】已知数列![]() 的首项
的首项![]() ,前
,前![]() 项和为
项和为![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前n项和Tn,并证明:1≤Tn<
的前n项和Tn,并证明:1≤Tn<![]() .
.
参考答案:
【答案】(1) an=3n-1.
(2) ![]() . 证明见解析.
. 证明见解析.
【解析】分析:(1)由递推关系式可得{an}是以3为公比的等比数列.且首项为1,则其通项公式为an=3n-1.
(2)由题意可得![]() ,错位相减可得
,错位相减可得![]() ,据此结合
,据此结合![]() 的单调性即可证得题中的结论.
的单调性即可证得题中的结论.
详解: (1)由an+1=2Sn+1,得an=2Sn-1+1(n≥2),
两式相减得an+1-an=2(Sn-Sn-1)=2an,
故an+1=3an(n≥2),
所以当n≥2时,{an}是以3为公比的等比数列.
因为a2=2S1+1=2a1+1=3,![]() =3,
=3,
所以{an}是首项为1,公比为3的等比数列,an=3n-1.
(2)由(1)知an=3n-1,故bn=log3an+1=log33n=n,![]() =
=![]() =n·
=n·![]() ,
,
Tn=1+2×![]() +3×
+3×![]() +4×
+4×![]() +…+n×
+…+n×![]() ,①
,①
![]() Tn=1×
Tn=1×![]() +2×
+2×![]() +3×
+3×![]() +…+(n-1)×
+…+(n-1)×![]() + n×
+ n×![]() ,②
,②
①-②,得![]() Tn=1+
Tn=1+![]() +
+![]() ,
,
所以Tn=![]() -(
-(![]() +
+![]() n)
n)![]() . 因为(
. 因为(![]() +
+![]() n)
n)![]() >0, 所以Tn=
>0, 所以Tn=![]() -(
-(![]() +
+![]() n)
n)![]() <
<![]() .
.
又因为Tn+1-Tn=![]() >0,所以数列{Tn}单调递增,所以(Tn)min=T1=1,所以1≤Tn<
>0,所以数列{Tn}单调递增,所以(Tn)min=T1=1,所以1≤Tn<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
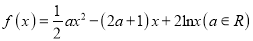 .
.(Ⅰ)求
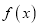 的单调区间;
的单调区间;(Ⅱ)设
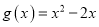 ,若对任意
,若对任意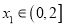 ,均存在
,均存在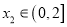 ,使得
,使得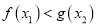 ,求
,求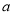 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:

(1)BE=EC;
(2)ADDE=2PB2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,
 .
.
(1)证明: A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
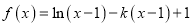 .
.(1)求函数
 的单调区间;
的单调区间;(2)若
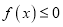 恒成立,试确定实数
恒成立,试确定实数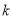 的取值范围;
的取值范围;(3)证明:
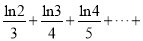
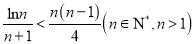 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知n为正整数,数列{an}满足an>0,4(n+1)an2﹣nan+12=0,设数列{bn}满足bn=
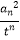
(1)求证:数列{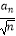 }为等比数列;
}为等比数列;
(2)若数列{bn}是等差数列,求实数t的值:
(3)若数列{bn}是等差数列,前n项和为Sn , 对任意的n∈N* , 均存在m∈N* , 使得8a12Sn﹣a14n2=16bm成立,求满足条件的所有整数a1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是抛物线
是抛物线 :
:  (
( )上一点,
)上一点,  是抛物线的焦点,
是抛物线的焦点,  且
且 .
.(1)求抛物线
 的方程;
的方程;(2)已知
 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 、
、 两点,以
两点,以 为圆心的圆
为圆心的圆 与直线
与直线 相切,试判断圆
相切,试判断圆 与直线
与直线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
相关试题

