【题目】在平面直角坐标系中,已知点![]() 为平面上一动点,
为平面上一动点,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)不过原点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 交点的纵坐标为1,求
交点的纵坐标为1,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 面积的最大值为
面积的最大值为![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
【解析】
试题分析:(Ⅰ)直接法求动点轨迹方程,先设动点坐标,再两点间距离公式及点到直线距离公式将条件用坐标表示,化简整理成椭圆标准方程;(Ⅱ)涉及弦中点问题,一般利用点差法求弦中点坐标与直线斜率的关系,本题由于弦中点与原点连线的斜率已知,所以可得弦所在直线斜率 .根据直线方程与椭圆方程联立方程组,结合韦达定理、弦长公式可得三角形底边长(用直线在![]() 轴上截距表示),再根据点到直线距离公式可得高(用直线在
轴上截距表示),再根据点到直线距离公式可得高(用直线在![]() 轴上截距表示),利用三角形面积公式可得面积关于直线在
轴上截距表示),利用三角形面积公式可得面积关于直线在![]() 轴上截距的函数关系式,最后根据基本不等式求最值,确定直线在
轴上截距的函数关系式,最后根据基本不等式求最值,确定直线在![]() 轴上截距,可得直线方程.
轴上截距,可得直线方程.
试题解析:解:(Ⅰ)由题意:![]() ,
,
又![]() ,即
,即![]() ,
,
化简整理得:![]()
所求曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)易得直线![]() 的方程:
的方程:![]() ,设
,设![]() .其中
.其中![]()
∵![]() 在椭圆上,
在椭圆上,
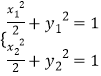 ,所以
,所以![]() ,
,
∴设直线![]() 的方程为:
的方程为:![]() .
.
联立: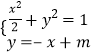 .整理得
.整理得![]() .
.
∵直线![]() 与椭圆有两个不同的交点且不过原点,
与椭圆有两个不同的交点且不过原点,
∴![]() ,解得:
,解得:![]() 且
且![]()
由韦达定理:![]()
∴![]()
![]()
![]()
![]() .
.
∵点![]() 到直线
到直线![]() 的距离为:
的距离为:![]() .
.
∴![]() .
.
当且仅当![]() 即
即![]() 时等号成立,满足(*)式
时等号成立,满足(*)式
所以![]() 面积的最大值为
面积的最大值为![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
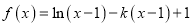 .
.(1)求函数
 的单调区间;
的单调区间;(2)若
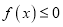 恒成立,试确定实数
恒成立,试确定实数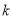 的取值范围;
的取值范围;(3)证明:
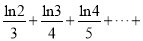
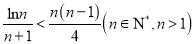 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知n为正整数,数列{an}满足an>0,4(n+1)an2﹣nan+12=0,设数列{bn}满足bn=
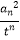
(1)求证:数列{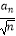 }为等比数列;
}为等比数列;
(2)若数列{bn}是等差数列,求实数t的值:
(3)若数列{bn}是等差数列,前n项和为Sn , 对任意的n∈N* , 均存在m∈N* , 使得8a12Sn﹣a14n2=16bm成立,求满足条件的所有整数a1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是抛物线
是抛物线 :
:  (
( )上一点,
)上一点,  是抛物线的焦点,
是抛物线的焦点,  且
且 .
.(1)求抛物线
 的方程;
的方程;(2)已知
 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 、
、 两点,以
两点,以 为圆心的圆
为圆心的圆 与直线
与直线 相切,试判断圆
相切,试判断圆 与直线
与直线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是抛物线
是抛物线 :
:  (
( )上一点,
)上一点,  是抛物线的焦点,
是抛物线的焦点,  且
且 .
.(1)求抛物线
 的方程;
的方程;(2)已知
 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 、
、 两点,以
两点,以 为圆心的圆
为圆心的圆 与直线
与直线 相切,试判断圆
相切,试判断圆 与直线
与直线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二阶矩阵M有特征值λ=8及对应的一个特征向量
 =[
=[  ],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值.
相关试题

