【题目】如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,![]() .
.

(1)证明: A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
参考答案:
【答案】(1)![]() ,见下.
,见下.
(2)1
【解析】
试题分析:(1)要证明![]() ⊥平面
⊥平面![]() ,只要证明
,只要证明![]() 垂直于平面
垂直于平面![]() 内的两条相交直线即可,由已知可证出
内的两条相交直线即可,由已知可证出![]() ⊥BD,取
⊥BD,取![]() 的中点为
的中点为![]() ,通过证明四边形
,通过证明四边形![]() 为正方形可证
为正方形可证![]() ⊥
⊥![]() .由线面垂直的判定定理问题得证;(2)由已知
.由线面垂直的判定定理问题得证;(2)由已知![]() 是三棱柱ABD﹣A1B1D1的高,由此能求出三棱柱ABD﹣A1B1D1的体积
是三棱柱ABD﹣A1B1D1的高,由此能求出三棱柱ABD﹣A1B1D1的体积
试题解析:(Ⅰ)∵四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=![]() ,由棱柱的性质可得BB1和DD1平行且相等,故四边形BB1D1D为平行四边形,故有BD和B1D1平行且相等.而BD不在平面CB1D1内,而B1D1在平面CB1D1内,∴BD∥平面CB1D1.同理可证,A1BCD1为平行四边形,A1B∥平面CB1D1.而BD和A1B是平面A1BD内的两条相交直线,故有平面A1BD∥平面CD1B1 .
,由棱柱的性质可得BB1和DD1平行且相等,故四边形BB1D1D为平行四边形,故有BD和B1D1平行且相等.而BD不在平面CB1D1内,而B1D1在平面CB1D1内,∴BD∥平面CB1D1.同理可证,A1BCD1为平行四边形,A1B∥平面CB1D1.而BD和A1B是平面A1BD内的两条相交直线,故有平面A1BD∥平面CD1B1 .
(Ⅱ)由题意可得A1O为三棱柱ABD﹣A1B1D1的高.三角形A1AO中,由勾股定理可得A1O=![]() =
=![]() =1,
=1,
∴三棱柱ABD﹣A1B1D1的体积V=S△ABDA1O=![]() A1O=
A1O=![]() ×1=1.
×1=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+x2﹣xlna(a>0且a≠1)
(1)求函数f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)单调区间;
(3)若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1(e是自然对数的底数),求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F.

(1)判断BE是否平分∠ABC,并说明理由;
(2)若AE=6,BE=8,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C1的方程为x2+(y+1)2=4,圆C2的圆心坐标为(2,1).
(1)若圆C1与圆C2相交于A,B两点,且|AB|=
 ,求点C1到直线AB的距离;
,求点C1到直线AB的距离;(2)若圆C1与圆C2相内切,求圆C2的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
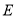 :
:  的左、右焦点分别为
的左、右焦点分别为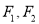 ,离心率
,离心率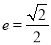 ,
, 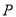 为椭圆
为椭圆 上的任意一点(不含长轴端点),且
上的任意一点(不含长轴端点),且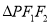 面积的最大值为1.
面积的最大值为1.(1)求椭圆
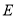 的方程;
的方程;(2)已知直线
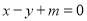 与椭圆
与椭圆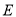 交于不同的两点
交于不同的两点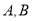 ,且线段
,且线段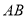 的中点不在圆
的中点不在圆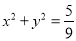 内,求
内,求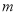 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆
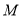 过定点
过定点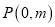
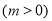 ,且与定直线
,且与定直线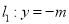 相切,动圆圆心
相切,动圆圆心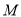 的轨迹方程为
的轨迹方程为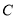 ,直线
,直线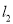 过点
过点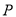 交曲线
交曲线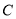 于
于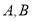 两点.
两点.(1)若
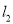 交
交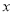 轴于点
轴于点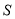 ,求
,求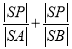 的取值范围;
的取值范围;(2)若
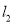 的倾斜角为
的倾斜角为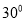 ,在
,在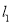 上是否存在点
上是否存在点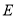 使
使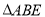 为正三角形?若能,求点
为正三角形?若能,求点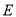 的坐标;若不能,说明理由.
的坐标;若不能,说明理由. -
科目: 来源: 题型:
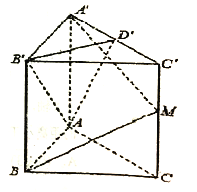
查看答案和解析>>【题目】直三棱柱
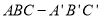 中,底面
中,底面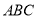 是边长为2的正三角形,
是边长为2的正三角形, 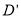 是棱
是棱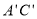 的中点,且
的中点,且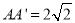 .
.
(1)若点
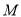 为棱
为棱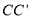 的中点,求异面直线
的中点,求异面直线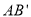 与
与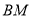 所成角的余弦值;
所成角的余弦值;(2)若点
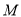 在棱
在棱 上,且
上,且 平面
平面 ,求线段
,求线段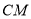 的长.
的长.
相关试题

