【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 时取得极值,求实数
时取得极值,求实数![]() 的值;
的值;
(2)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由![]() ,依题意有:
,依题意有:![]() ,即
,即![]() ,通过检验满足在
,通过检验满足在![]() 时取得极值. (2)依题意有:
时取得极值. (2)依题意有:![]() 从而
从而![]() ,令
,令![]() ,得:
,得:![]() ,
,![]() ,通过讨论①
,通过讨论①![]() 和②
和②![]() ,进而求出
,进而求出![]() 的取值范围.
的取值范围.
试题解析:
(1)![]() ,
,
依题意有![]() ,即
,即![]() ,解得
,解得![]() .
.
检验:当![]() 时,
时,![]() .
.
此时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,满足在
上单调递增,满足在![]() 时取得极值.
时取得极值.
综上可知![]() .
.
(2)依题意可得:![]() 对任意
对任意![]() 恒成立等价转化为
恒成立等价转化为![]() 在
在![]() 上恒成立.
上恒成立.
因为![]() ,
,
令![]() 得:
得:![]() ,
,![]() .
.
①当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 上单调递增,
上单调递增,
于是![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
②当![]() ,即
,即![]() 时,
时,![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
于是![]() ,不合题意,此时
,不合题意,此时![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 ,
, .
. 是自然对数的底数.
是自然对数的底数.(1)求曲线
 在
在 处的切线方程为
处的切线方程为 ,求实数
,求实数 ,
, 的值;
的值;(2)①若
 时,函数
时,函数 既有极大值又有极小值,求实数
既有极大值又有极小值,求实数 的取值范围;
的取值范围;②若
 ,
, ,若
,若 对一切正实数
对一切正实数 恒成立,求实数
恒成立,求实数 的取值范围(用
的取值范围(用 表示).
表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
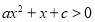 的解集为
的解集为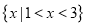 .
.(1)求
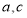 的值;
的值;(2)若不等式
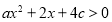 的解集为
的解集为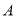 ,不等式
,不等式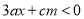 的解集为
的解集为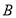 ,且
,且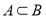 ,求实数
,求实数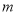 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为实数).
为实数).(1)当
 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;(2)设函数
 (其中
(其中 为常数),若函数
为常数),若函数 在区间
在区间 上不存在极值,且存在
上不存在极值,且存在 满足
满足 ,求
,求 的取值范围;
的取值范围;(3)已知
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.

(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第
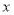 天的实验需投入实验费用为
天的实验需投入实验费用为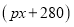 元
元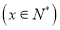 ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.(1)求
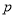 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;(2)现有某知名企业对该项实验进行赞助,实验
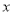 天共赞助
天共赞助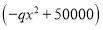 元
元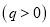 .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求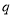 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费) -
科目: 来源: 题型:
查看答案和解析>>【题目】在
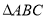 中,角
中,角 所对的边分别为
所对的边分别为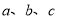 ,且
,且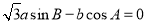 .
.(1)求角
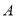 的大小;
的大小;(2)若
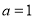 ,求
,求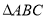 周长的最大值.
周长的最大值.
相关试题

