【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.![]() 是自然对数的底数.
是自然对数的底数.
(1)求曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)①若![]() 时,函数
时,函数![]() 既有极大值又有极小值,求实数
既有极大值又有极小值,求实数![]() 的取值范围;
的取值范围;
②若![]() ,
,![]() ,若
,若![]() 对一切正实数
对一切正实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
参考答案:
【答案】(1)![]() ,
,![]() .(2)①
.(2)①![]() ,②
,②![]()
【解析】
试题分析:(1)由导数几何意义得![]() ,求函数导数
,求函数导数![]() 得等量关系
得等量关系![]() ,再根据切点既在切线上也在曲线上得
,再根据切点既在切线上也在曲线上得![]() ,解方程组得实数
,解方程组得实数![]() ,
,![]() 的值(2)①先求函数导数得
的值(2)①先求函数导数得![]() ,转化为方程
,转化为方程![]() 有两个零点,再利用导数研究函数
有两个零点,再利用导数研究函数![]() 单调性变化规律:
单调性变化规律:![]() 上减,
上减,![]() 上减增,即
上减增,即![]() 时取最小值,因此
时取最小值,因此![]() ,最后列表分析证明,②先化简不等式
,最后列表分析证明,②先化简不等式![]() ,再探求实数
,再探求实数![]() 的取值范围:取
的取值范围:取![]() 得
得![]() .由于
.由于![]() ,
,![]() ,所以
,所以![]() ,因此
,因此![]() 时不等式恒成立
时不等式恒成立
试题解析:(1)由题意知曲线![]() 过点
过点![]() ,且
,且![]() ;
;
又因为![]() ,
,
则有![]() 解得
解得![]() ,
,![]() .
.
(2)①当![]() 时,函数
时,函数![]() 的导函数
的导函数![]() ,
,
若![]() 时,得
时,得![]() ,
,
设![]() (
(![]() ),
),
由![]() ,得
,得![]() ,
,![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上为减函数,
上为减函数,![]() ;
;
仅当![]() 时,
时,![]() 有两个不同的解,设为
有两个不同的解,设为![]() ,
,![]() (
(![]() ).
).
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
此时,函数![]() 既有极大值又有极小值.
既有极大值又有极小值.
②由题意![]() 对一切正实数
对一切正实数![]() 恒成立,
恒成立,
取![]() 得
得![]() .
.
下证![]() 对一切正实数
对一切正实数![]() 恒成立.
恒成立.
首先,证明![]() ,设函数
,设函数![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;得
;得![]() ,即
,即![]() ,
,
当且仅当都在![]() 处取到等号.
处取到等号.
再证![]() ,设
,设![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;得
;得![]() ,即
,即![]() ,
,
当且仅当都在![]() 处取到等号.
处取到等号.
由上可得![]() ,所以
,所以![]() ,
,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品
 和产品
和产品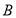 需要甲、乙两种新型材料,生产一件产品
需要甲、乙两种新型材料,生产一件产品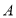 需要甲材料1.5
需要甲材料1.5 ,乙材料1
,乙材料1 ,用5个工时,生产一件产品需要甲材料0.5
,用5个工时,生产一件产品需要甲材料0.5 ,乙材料0.3
,乙材料0.3 ,用3个工时,生产一件产品的利润为2100元,生产一件产品的利润为900元.该企业现有甲材料150
,用3个工时,生产一件产品的利润为2100元,生产一件产品的利润为900元.该企业现有甲材料150 ,乙材料90
,乙材料90 ,则在不超过600个工时的条件下,生产产品
,则在不超过600个工时的条件下,生产产品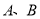 的利润之和的最大值为____________元.
的利润之和的最大值为____________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,
, .
.(1)当
 ,
, 时,求函数
时,求函数 的单调区间;
的单调区间;(2)当
 时,若
时,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)设函数
 的图象在两点
的图象在两点 ,
, 处的切线分别为
处的切线分别为 ,
, ,若
,若 ,
, ,且
,且 ,求实数
,求实数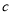 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
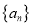 满足
满足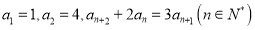 .
.(1)求证:数列
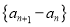 是等比数列,并求
是等比数列,并求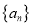 的通项公式;
的通项公式;(2)记数列
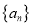 的前
的前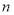 项和
项和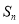 ,求使得
,求使得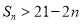 成立的最小整数
成立的最小整数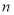 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
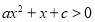 的解集为
的解集为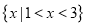 .
.(1)求
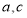 的值;
的值;(2)若不等式
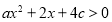 的解集为
的解集为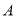 ,不等式
,不等式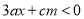 的解集为
的解集为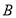 ,且
,且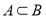 ,求实数
,求实数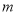 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为实数).
为实数).(1)当
 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;(2)设函数
 (其中
(其中 为常数),若函数
为常数),若函数 在区间
在区间 上不存在极值,且存在
上不存在极值,且存在 满足
满足 ,求
,求 的取值范围;
的取值范围;(3)已知
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
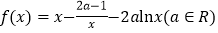 .
.(1)若函数
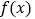 在
在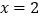 时取得极值,求实数
时取得极值,求实数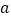 的值;
的值;(2)若
 对任意
对任意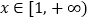 恒成立,求实数
恒成立,求实数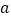 的取值范围.
的取值范围.
相关试题

