【题目】在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,求
,求![]() 周长的最大值.
周长的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)已知等式利用正弦定理化简,由![]() 求出
求出![]() 的值,即可确定出
的值,即可确定出![]() 的度数;(2)由余弦定理列出关系式,得到
的度数;(2)由余弦定理列出关系式,得到![]() ,化简为
,化简为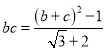 ,用基本不等式可得到
,用基本不等式可得到![]() 的最值,得到周长的最大值.
的最值,得到周长的最大值.
试题解析:(1)![]() ,即为
,即为![]() ,
,
代入正弦定理得:![]() ........................2分
........................2分
又![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() ................4分
................4分
又![]() ,∴
,∴![]() ............6分
............6分
(2)由余弦定理得![]() ,即
,即![]() ,
,
化简得,![]() ,.....................7分
,.....................7分
∵![]() ,∴
,∴![]() ,∴
,∴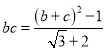 ,.........8分
,.........8分
∵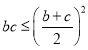 ,∴
,∴ ,当且仅当
,当且仅当![]() 时取等号成立,
时取等号成立,
解得![]() ,
,
∴![]() (当且仅当
(当且仅当![]() 时取等号),.......................11分
时取等号),.......................11分
∴![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
∴![]() 周长的最大值为
周长的最大值为![]() .............................12分
.............................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
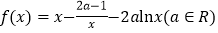 .
.(1)若函数
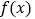 在
在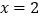 时取得极值,求实数
时取得极值,求实数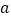 的值;
的值;(2)若
 对任意
对任意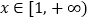 恒成立,求实数
恒成立,求实数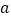 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.

(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第
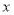 天的实验需投入实验费用为
天的实验需投入实验费用为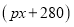 元
元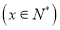 ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.(1)求
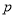 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;(2)现有某知名企业对该项实验进行赞助,实验
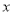 天共赞助
天共赞助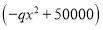 元
元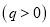 .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求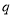 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
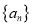 的前
的前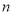 项和为
项和为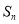 ,公差
,公差 ,且
,且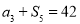 ,
,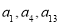 成等比数列.
成等比数列.(1)求数列
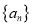 的通项公式;
的通项公式;(2)设
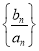 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列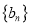 的前
的前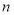 项和
项和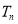 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
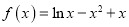 .
.(1)求函数
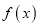 的单调区间;
的单调区间; (2)证明当
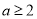 时,关于
时,关于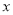 的不等式
的不等式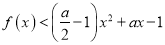 恒成立;
恒成立;(3)若正实数
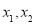 满足
满足 ,证明
,证明 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了
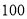 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间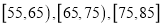 内的频率之比为
内的频率之比为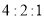 .
.(1) 求顾客年龄值落在区间
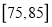 内的频率;
内的频率; (2) 拟利用分层抽样从年龄在
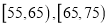 的顾客中选取
的顾客中选取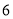 人召开一个座谈会,现从这
人召开一个座谈会,现从这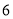 人中选出
人中选出 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.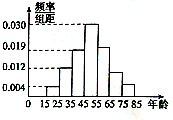
相关试题

