【题目】设Sn为数列{an}的前n项的和,且Sn =![]() (an -1)(n∈N*), 数列{bn }的通项公式bn = 4n+5.
(an -1)(n∈N*), 数列{bn }的通项公式bn = 4n+5.
①求证:数列{an }是等比数列;
②若d∈{a1 ,a2 ,a3 ,……}∩{b1 ,b2 ,b3 ,……},则称d为数列{an }和{bn }的公共项,按它们在原数列中的先后顺序排成一个新的数列{dn },求数列{dn }的通项公式.
参考答案:
【答案】(1)见解析(2)dn=9n.
【解析】
①利用公式an=Sn-Sn-1代入得出an与an-1之间的关系.再根据等比数列定义进行证明,②令ak=bm ,得![]() 可得
可得![]() ,因此数列{dn }为首项与公比为9的等比数列,最后根据等比数列通项公式得结果.
,因此数列{dn }为首项与公比为9的等比数列,最后根据等比数列通项公式得结果.
解:①当n=1时,由a1=S1=![]() ,得出a1=3.当n≥2时,
,得出a1=3.当n≥2时,![]()
②由an=3n,得:
![]()

因此dn=9×9n—1=9n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
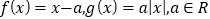 .
.(1)设
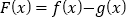 .
.①若
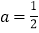 ,求函数
,求函数 的零点;
的零点;②若函数
 存在零点,求
存在零点,求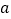 的取值范围.
的取值范围.(2)设
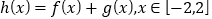 ,若对任意
,若对任意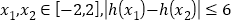 恒成立,试求
恒成立,试求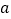 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是方程
是方程 的两根, 数列
的两根, 数列 是公差为正的等差数列,数列
是公差为正的等差数列,数列 的前
的前 项和为
项和为 ,且
,且 .
.(1)求数列
 的通项公式;
的通项公式; (2)记
 ,求数列
,求数列 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣e﹣x , 下列命题正确的有 . (写出所有正确命题的编号)
①f(x)是奇函数;
②f(x)在R上是单调递增函数;
③方程f(x)=x2+2x有且仅有1个实数根;
④如果对任意x∈(0,+∞),都有f(x)>kx,那么k的最大值为2. -
科目: 来源: 题型:
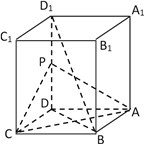
查看答案和解析>>【题目】如图,长方体ABCD—A1B1C1D1中,试在DD1确定一点P,使得直线BD1∥平面PAC,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
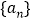 为等差数列,
为等差数列, ,
,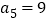 .
.(1) 求数列
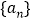 的通项公式;
的通项公式;(2)求数列
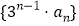 的前n项和
的前n项和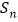 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面五边形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE是边长为2的正三角形.现将△ADE沿AD折起,得到四棱锥E﹣ABCD(如图2),且DE⊥AB.
(Ⅰ)求证:平面ADE⊥平面ABCD;
(Ⅱ)求平面BCE和平面ADE所成锐二面角的大小;
(Ⅲ)在棱AE上是否存在点F,使得DF∥平面BCE?若存在,求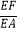 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.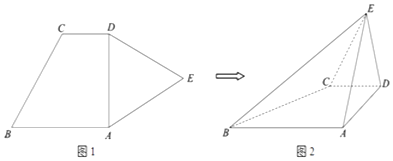
相关试题

