搜索
【题目】已知数列
为等差数列，
，
.
（1） 求数列的通项公式;
（2）求数列
的前n项和
.
参考答案：
【答案】（1）
；（2）
.
【解析】试题分析：利用等差数列通项公式列出方程组，求出首项和公差，由此能求出数列
的
通项公式；（2）由（1）可得
，利用错位相减法及等比数列前
项和公式能求出数列
的前n项和
.
试题解析： (1)设数列
的公差为
，依题意得方程组
解得
.
所以的通项公式为
.
（2）由（1）可得，
－得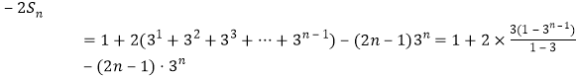
所以
.
【 方法点睛】本题主要考查等差数列的通项公式、等比数列的求和公式以及错位相减法求数列的前 项和，属于中档题.一般地，如果数列是等差数列，
是等比数列，求数列
的前项和时，可采用“错位相减法”求和，一般是和式两边同乘以等比数列的公比，然后作差求解, 在写出“”
与“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
”的表达式.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=ex﹣e﹣x ， 下列命题正确的有 ． （写出所有正确命题的编号）
①f（x）是奇函数；
②f（x）在R上是单调递增函数；
③方程f（x）=x2+2x有且仅有1个实数根；
④如果对任意x∈（0，+∞），都有f（x）＞kx，那么k的最大值为2． -
科目： 来源： 题型：
查看答案和解析>>【题目】设Sn为数列{an}的前ｎ项的和，且Sn =
(an －1)(n∈N*)， 数列{bn }的通项公式bn = 4n+5.①求证：数列{an }是等比数列；
②若d∈{a1 ，a2 ，a3 ，……}∩{b1 ，b2 ，b3 ，……}，则称d为数列{an }和{bn }的公共项，按它们在原数列中的先后顺序排成一个新的数列{dn }，求数列{dn }的通项公式.
-
科目： 来源： 题型：
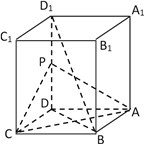
查看答案和解析>>【题目】如图，长方体ABCD—A1B1C1D1中，试在DD1确定一点P，使得直线BD1∥平面PAC，并证明你的结论.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，平面五边形ABCDE中，AB∥CD，∠BAD=90°，AB=2，CD=1，△ADE是边长为2的正三角形．现将△ADE沿AD折起，得到四棱锥E﹣ABCD（如图2），且DE⊥AB．
（Ⅰ）求证：平面ADE⊥平面ABCD；
（Ⅱ）求平面BCE和平面ADE所成锐二面角的大小；
（Ⅲ）在棱AE上是否存在点F，使得DF∥平面BCE？若存在，求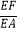
的值；若不存在，请说明理由．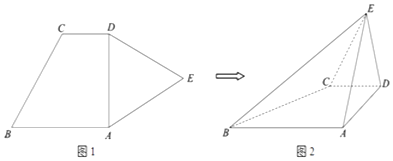
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司购买了A，B，C三种不同品牌的电动智能送风口罩．为了解三种品牌口罩的电池性能，现采用分层抽样的方法，从三种品牌的口罩中抽出25台，测试它们一次完全充电后的连续待机时长，统计结果如下（单位：小时）：
A
4
4
4.5
5
5.5
6
6
B
4.5
5
6
6.5
6.5
7
7
7.5
C
5
5
5.5
6
6
7
7
7.5
8
8
（1）已知该公司购买的C品牌电动智能送风口罩比B品牌多200台，求该公司购买的B品牌电动智能送风口罩的数量；
（2）从A品牌和B品牌抽出的电动智能送风口罩中，各随机选取一台，求A品牌待机时长高于B品牌的概率；
（3）再从A，B，C三种不同品牌的电动智能送风口罩中各随机抽取一台，它们的待机时长分别是a，b，c（单位：小时）．这3个新数据与表格中的数据构成的新样本的平均数记为μ1 ， 表格中数据的平均数记为μ0 ． 若μ0≤μ1 ， 写出a+b+c的最小值（结论不要求证明）． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）对任意
，都有xln（kx）﹣kx+1≤mx，求m的取值范围．
相关试题
