【题目】已知函数f(x)=ex﹣e﹣x , 下列命题正确的有 . (写出所有正确命题的编号)
①f(x)是奇函数;
②f(x)在R上是单调递增函数;
③方程f(x)=x2+2x有且仅有1个实数根;
④如果对任意x∈(0,+∞),都有f(x)>kx,那么k的最大值为2.
参考答案:
【答案】①②④
【解析】解:根据题意,依次分析4个命题:
对于①、f(x)=ex﹣e﹣x , 定义域是R,且f(﹣x)=e﹣x﹣ex=﹣f(x),f(x)是奇函数;故①正确;
对于②、若f(x)=ex﹣e﹣x , 则f′(x)=ex+e﹣x>0,故f(x)在R递增;故②正确;
对于③、f(x)=x2+2x,令g(x)=ex﹣e﹣x﹣x2﹣2x,
令x=0可得,g(0)=0,即方程f(x)=x2+2x有一根x=0,
g(3)=e3﹣ ![]() ﹣13<0,g(4)=e4﹣
﹣13<0,g(4)=e4﹣ ![]() ﹣20>0,
﹣20>0,
则方程f(x)=x2+2x有一根在(3,4)之间,
故③错误;
对于④、如果对任意x∈(0,+∞),都有f(x)>kx,即ex﹣e﹣x﹣kx>0恒成立,
令h(x)=ex﹣e﹣x﹣kx,且h(0)=0,
若h(x)>0恒成立,则必有h′(x)=ex+e﹣x﹣k>0恒成立,
若ex+e﹣x﹣k>0,即k<ex+e﹣x=ex+ ![]() 恒成立,
恒成立,
而ex+ ![]() ≥2,若有k<2,
≥2,若有k<2,
故④正确;
综合可得:①②④正确;
所以答案是:①②④.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系,曲线C:ρ2﹣4ρcosθ+1=0,直线l:
 (t为参数,0≤α<π).
(t为参数,0≤α<π).
(1)求曲线C的参数方程;
(2)若直线l与曲线C相切,求直线l的倾斜角及切点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
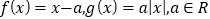 .
.(1)设
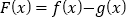 .
.①若
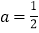 ,求函数
,求函数 的零点;
的零点;②若函数
 存在零点,求
存在零点,求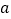 的取值范围.
的取值范围.(2)设
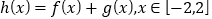 ,若对任意
,若对任意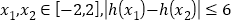 恒成立,试求
恒成立,试求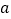 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是方程
是方程 的两根, 数列
的两根, 数列 是公差为正的等差数列,数列
是公差为正的等差数列,数列 的前
的前 项和为
项和为 ,且
,且 .
.(1)求数列
 的通项公式;
的通项公式; (2)记
 ,求数列
,求数列 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设Sn为数列{an}的前n项的和,且Sn =
 (an -1)(n∈N*), 数列{bn }的通项公式bn = 4n+5.
(an -1)(n∈N*), 数列{bn }的通项公式bn = 4n+5.①求证:数列{an }是等比数列;
②若d∈{a1 ,a2 ,a3 ,……}∩{b1 ,b2 ,b3 ,……},则称d为数列{an }和{bn }的公共项,按它们在原数列中的先后顺序排成一个新的数列{dn },求数列{dn }的通项公式.
-
科目: 来源: 题型:
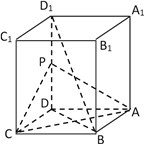
查看答案和解析>>【题目】如图,长方体ABCD—A1B1C1D1中,试在DD1确定一点P,使得直线BD1∥平面PAC,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
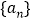 为等差数列,
为等差数列, ,
,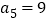 .
.(1) 求数列
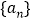 的通项公式;
的通项公式;(2)求数列
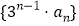 的前n项和
的前n项和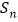 .
.
相关试题

