【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为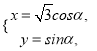 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据sin2+cos2θ=1,x=ρcosθ,y=ρsinθ.将参数方程和极坐标方程化成直角坐标方程;
(2)由题意可得当直线x+y-4=0的平行线与椭圆相切时,|PQ|取得最值.设与直线x+y-4=0平行的直线方程为x+y+t=0,代入椭圆方程,运用判别式为0,求得t,再由平行线的距离公式,可得|PQ|的最小值.
试题解析:
(1)![]() ;
; ![]()
(2)解法1:设![]() ,
,
它到![]() 的距离
的距离
解法2:平移直线![]() 到
到![]() 与椭圆相切,则
与椭圆相切,则
![]()
![]() …………8分
…………8分
![]() 得
得![]() …………10分,显然
…………10分,显然![]() 时,
时,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验,甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在
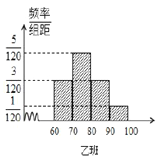
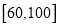 区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.
区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.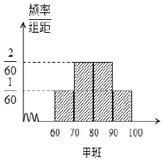
(1)根据以上信息填好
 联表,并判断出有多大的把握认为学生成绩优良与班级有关?
联表,并判断出有多大的把握认为学生成绩优良与班级有关?(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选3人来作书面发言,求发言人至少有2人来自甲班的概率.
(以下临界值及公式仅供参考)
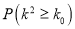
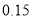
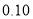
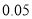
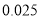
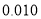
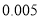
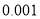
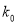
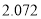
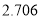
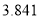
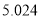
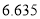
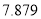
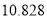
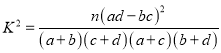 ,
, 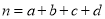 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】现安排甲乙丙丁戊5名学生分别担任语文、数学、英语、物理、化学学科的科代表,要求甲不当语文科代表,乙不当数学科代表,若丙当物理科代表则丁必须当化学科代表,则不同的选法共有多少种( )
A. 53 B. 67 C. 85 D. 91
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图.规定:成绩不低于120分时为优秀成绩.

(1)从甲班的样本中有放回的随机抽取 2 个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为
 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
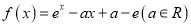 ,其中
,其中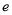 是自然对数的底数.
是自然对数的底数.(1)若
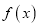 在
在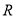 上为单调函数,求实数
上为单调函数,求实数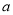 的取值范围;
的取值范围;(2)若
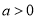 ,求证:
,求证: 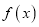 有唯一零点的充要条件是
有唯一零点的充要条件是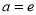 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设P是圆
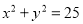 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且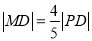 ,
,(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为
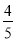 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.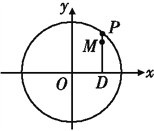
-
科目: 来源: 题型:
查看答案和解析>>【题目】在刚刚结束的五市联考中,某校对甲、乙两个文科班的数学成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,成绩统计后,得到如下的
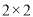 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为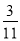 .
.班级
优秀
非优秀
合计
甲班
18
乙班
43
合计
110
(1)请完成上面的列联表;
(2)请问:是否有
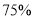 的把握认为“数学成绩与所在的班级有关系”?
的把握认为“数学成绩与所在的班级有关系”?(3)用分层抽样的方法从甲、乙两个文科班的数学成绩优秀的学生中抽取5名学生进行调研,然后再从这5名学生中随机抽取2名学生进行谈话,求抽到的2名学生中至少有1名乙班学生的概率.
参考公式:
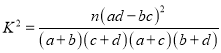 (其中
(其中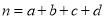 )
)参考数据:

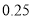

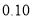
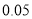
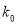

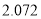
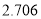
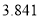
相关试题

