【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验,甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在![]() 区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.
区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.
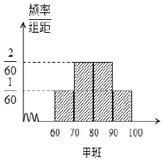
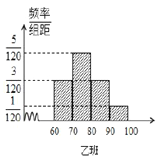
(1)根据以上信息填好![]() 联表,并判断出有多大的把握认为学生成绩优良与班级有关?
联表,并判断出有多大的把握认为学生成绩优良与班级有关?
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选3人来作书面发言,求发言人至少有2人来自甲班的概率.
(以下临界值及公式仅供参考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
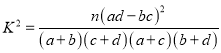 ,
, ![]() .
.
参考答案:
【答案】(1) 有![]() 的把握认为学生成绩优良与班级有关;(2)
的把握认为学生成绩优良与班级有关;(2)![]() .
.
【解析】试题分析:(1)根据所给数据可得列联表,利用公式计算![]() 的值,对照临界值即可得结论;
的值,对照临界值即可得结论;
(2)利用分层抽样原理与列举法计算基本事件数,求出对应的概率值
试题解析:
(1)
是否优良 班级 | 优良(人数) | 非优良(人数) | 合计 |
甲 | 30 | 30 | 60 |
乙 | 20 | 40 | 60 |
合计 | 50 | 70 | 120 |
![]() ,
,
则有![]() 的把握认为学生成绩优良与班级有关.
的把握认为学生成绩优良与班级有关.
(2) ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为
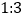 ,且成绩分布在
,且成绩分布在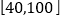 ,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见下图)
,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见下图)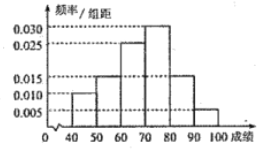
(Ⅰ)求所抽取样本的平均值
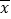 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);(Ⅱ)填写下面的
 列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?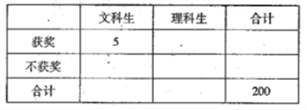
附表及公式:
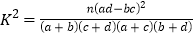 ,其中
,其中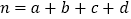
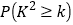
0.15
0.10
0.05
0.025
0.010
0.005
0.001
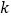
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
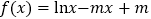 .
.(I)求函数
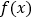 的单调区间;
的单调区间;(II)若
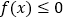 在
在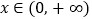 上恒成立,求实数
上恒成立,求实数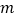 的取值范围;
的取值范围;(III)在(II)的条件下,对任意的
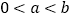 ,求证:
,求证: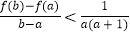 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,第一道审核、第二道审核、第三道审核通过的概率分别为
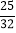 ,
, ,
, ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.(1)求审核过程中只通过两道程序的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】现安排甲乙丙丁戊5名学生分别担任语文、数学、英语、物理、化学学科的科代表,要求甲不当语文科代表,乙不当数学科代表,若丙当物理科代表则丁必须当化学科代表,则不同的选法共有多少种( )
A. 53 B. 67 C. 85 D. 91
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图.规定:成绩不低于120分时为优秀成绩.

(1)从甲班的样本中有放回的随机抽取 2 个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为
 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
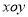 中,曲线
中,曲线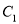 的参数方程为
的参数方程为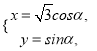 (
(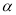 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以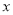 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线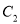 的极坐标方程为
的极坐标方程为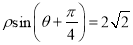 .
.(1)写出
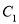 的普通方程和
的普通方程和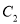 的直角坐标方程;
的直角坐标方程;(2)设点
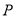 在
在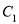 上,点
上,点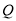 在
在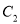 上,求
上,求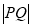 的最小值.
的最小值.
相关试题

