【题目】在刚刚结束的五市联考中,某校对甲、乙两个文科班的数学成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,成绩统计后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
班级 | 优秀 | 非优秀 | 合计 |
甲班 | 18 | ||
乙班 | 43 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)请问:是否有![]() 的把握认为“数学成绩与所在的班级有关系”?
的把握认为“数学成绩与所在的班级有关系”?
(3)用分层抽样的方法从甲、乙两个文科班的数学成绩优秀的学生中抽取5名学生进行调研,然后再从这5名学生中随机抽取2名学生进行谈话,求抽到的2名学生中至少有1名乙班学生的概率.
参考公式: 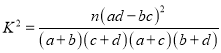 (其中
(其中![]() )
)
参考数据:
|
|
|
|
|
|
|
|
|
|
参考答案:
【答案】(1)见解析;(2)有75%的把握认为“数学成绩与所在的班级有关系”;(3) ![]() .
.
【解析】试题分析:(1)利用已知条件直接填写联列表即可;(2)利用公式 ,与临界值比较求出
,与临界值比较求出![]() ,即可判断“数学成绩与所在的班级有关系;(3)从甲班成绩优秀的学生中抽取
,即可判断“数学成绩与所在的班级有关系;(3)从甲班成绩优秀的学生中抽取![]() 名,分别记为
名,分别记为![]() ,从乙班成绩优秀的学生中抽取
,从乙班成绩优秀的学生中抽取![]() 名,分别为
名,分别为![]() ,列出所有基本事件,设“抽到的
,列出所有基本事件,设“抽到的![]() 名学生中至少有
名学生中至少有![]() 名乙班学生”为事件
名乙班学生”为事件![]() ,求出事件
,求出事件![]() 包含的基本事件个数,然后求解概率.
包含的基本事件个数,然后求解概率.
试题解析:(1)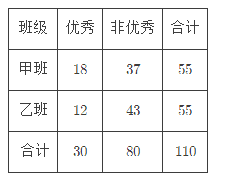
(2)由题意得![]()
所以75%的把握认为“数学成绩与所在的班级有关系”
(3)因为甲,乙两个班数学成绩优秀的学生人数的比例为![]() ,所以从甲班成绩优秀的学生中抽取3名,分别记为
,所以从甲班成绩优秀的学生中抽取3名,分别记为![]() ,从乙班成绩优秀的学生中抽取2名,分别记为
,从乙班成绩优秀的学生中抽取2名,分别记为![]() ,则从抽取的5名学生中随机抽取2名学生的基本事件有
,则从抽取的5名学生中随机抽取2名学生的基本事件有
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10个
,共10个
设“抽到2名学生中至少有1名乙班学生”为事件A,则事件A包含的基本事件有
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共7个,所以
,共7个,所以![]() ,即抽到2名学生中至少有1名乙班学生的概率是
,即抽到2名学生中至少有1名乙班学生的概率是![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
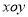 中,曲线
中,曲线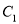 的参数方程为
的参数方程为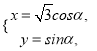 (
(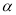 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以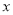 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线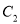 的极坐标方程为
的极坐标方程为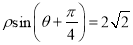 .
.(1)写出
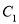 的普通方程和
的普通方程和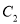 的直角坐标方程;
的直角坐标方程;(2)设点
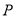 在
在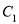 上,点
上,点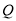 在
在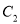 上,求
上,求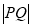 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
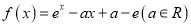 ,其中
,其中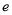 是自然对数的底数.
是自然对数的底数.(1)若
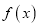 在
在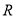 上为单调函数,求实数
上为单调函数,求实数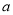 的取值范围;
的取值范围;(2)若
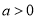 ,求证:
,求证: 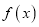 有唯一零点的充要条件是
有唯一零点的充要条件是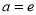 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设P是圆
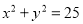 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且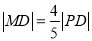 ,
,(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为
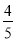 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.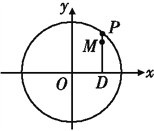
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,
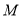 是
是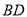 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.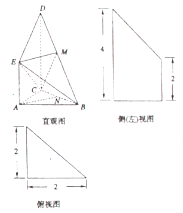
(1)求出该几何体的体积;
(2)若
 是
是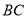 的中点,求证:
的中点,求证: 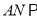 平面
平面 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以坐标原点为极点,
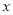 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线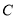 的极坐标方程为
的极坐标方程为 ,过点
,过点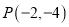 的直线
的直线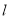 的参数方程为
的参数方程为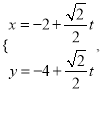 (
(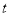 为参数),直线
为参数),直线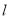 与曲线
与曲线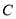 相交于
相交于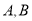 两点.
两点.(1)写出曲线
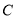 的直角坐标方程和直线
的直角坐标方程和直线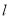 的普通方程;
的普通方程;(2)若
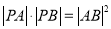 ,求
,求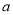 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
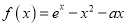 .
.(1)
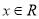 时,证明:
时,证明: 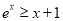 ;
;(2)当
 时,直线
时,直线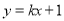 和曲线
和曲线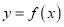 切于点
切于点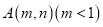 ,求实数
,求实数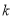 的值;
的值;(3)当
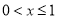 时,不等式
时,不等式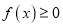 恒成立,求实数
恒成立,求实数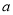 的取值范围.
的取值范围.
相关试题

