【题目】记![]() 表示
表示![]() 中的最大值,如
中的最大值,如![]() ,已知函数
,已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的值域;
上的值域;
(2)试探讨是否存在实数![]() , 使得
, 使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;
的取值范围;
若不存在,说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据题意,明确给定范围上的![]() 的表达式,然后求值域;(2)根据题意,明确给定范围上的
的表达式,然后求值域;(2)根据题意,明确给定范围上的![]() 的表达式,然后恒成立问题就转化为最值问题.
的表达式,然后恒成立问题就转化为最值问题.
试题解析:(1)设![]() ,.............1分
,.............1分
令![]() ,得
,得![]() 递增;令
递增;令![]() ,得
,得![]() 递减,.................2分
递减,.................2分
∴![]() ,∴
,∴![]() ,.......................3分
,.......................3分
即![]() ,∴
,∴![]() .............4分
.............4分
故函数![]() 在
在![]() 上的值域为
上的值域为![]() ...........................5分
...........................5分
(2)①当![]() 时,
时,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .................................................. 6分
.................................................. 6分
若![]() ,对
,对![]() 恒成立,则
恒成立,则![]() 对
对![]() 恒成立,
恒成立,
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() 递增;令
递增;令![]() ,得
,得![]() 递减.
递减.
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ....9分
....9分
②当![]() 时,由(1)知
时,由(1)知![]() ,对
,对![]() 恒成立,
恒成立,
若![]() 对
对![]() 恒成立,则
恒成立,则![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,这显然不可能.
恒成立,这显然不可能.
即当![]() 时,不满足
时,不满足![]() 对
对![]() 恒成立,.........................11分
恒成立,.........................11分
故存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立,且
恒成立,且![]() 的取值范围为
的取值范围为![]() .......12分
.......12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2=4,直线l:x+y=2.以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
(1)将圆C和直线l的方程化为极坐标方程;
(2)P是l上的点,射线OP交圆C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,当点P在l上移动时,求点Q轨迹的极坐标方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分) 已知椭圆
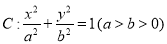 经过点
经过点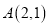 ,离心率为
,离心率为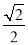 ,过点
,过点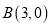 的直线
的直线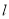 与椭圆
与椭圆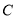 交于不同的两点
交于不同的两点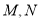 .
.(1)求椭圆
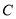 的方程;
的方程;(2)求
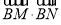 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l:
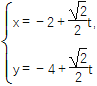 (t为参数)与曲线C相交于M,N两点.
(t为参数)与曲线C相交于M,N两点.(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,如果集合AS,那么S的子集A的补集为SA={x|x∈S,且xA}.类似地,对于集合A、B,我们把集合{x|x∈A,且xB}叫作集合A与B的差集,记作A-B.据此回答下列问题:
(1)若A={1,2,3,4},B={3,4,5,6},求A-B;
(2)在下列各图中用阴影表示集合A-B.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在极坐标系中点C的极坐标为
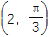 .
.(1)求出以点C为圆心,半径为2的圆的极坐标方程(写出解题过程)并画出图形;
(2)在直角坐标系中,以圆C所在极坐标系的极点为原点,极轴为x轴的正半轴建立直角坐标系,点P是圆C上任意一点,Q(5,-
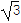 ),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程.
),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:
 .估计该校学生每周平均体育运动时间超过4小时的概率;
.估计该校学生每周平均体育运动时间超过4小时的概率;
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.

0.10
0.05
0.010
0.005
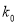
2.706
3.841
6.635
7.879
附:

相关试题

