【题目】某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为: ![]() .估计该校学生每周平均体育运动时间超过4小时的概率;
.估计该校学生每周平均体育运动时间超过4小时的概率;

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附: 
参考答案:
【答案】(1)90(2)0.75(3)有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
【解析】试题分析:(1)![]() 应收集
应收集![]() 位女生的样本数据;(2)由图得每周平均体育运动超过
位女生的样本数据;(2)由图得每周平均体育运动超过![]() 小时的频率为
小时的频率为![]() 该校学生每周平均体育运动时间超过
该校学生每周平均体育运动时间超过![]() 小时的概率的估计值为
小时的概率的估计值为![]() ;(3)求出列联表代入公式可得
;(3)求出列联表代入公式可得![]() 有
有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
试题解析: (1)![]() ,所以应收集
,所以应收集![]() 位女生的样本数据;
位女生的样本数据;
(2)由频率分布直方图得每周平均体育运动超过![]() 小时的频率为
小时的频率为![]() ,所以该校学生每周平均体育运动时间超过
,所以该校学生每周平均体育运动时间超过![]() 小时的概率的估计值为
小时的概率的估计值为![]() ;
;
(3)由(2)知,![]() 位学生有
位学生有![]() (位)的每周平均体育运动时间超过
(位)的每周平均体育运动时间超过![]() 小时,
小时,![]() 人的每周平均体育运动时间不超过
人的每周平均体育运动时间不超过![]() 小时,又因为样本数据中有
小时,又因为样本数据中有![]() 份是关于男生的,
份是关于男生的,![]() 份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过 |
|
|
|
每周平均体育运动时间超过 |
|
|
|
总计 |
|
|
|
结合列联表可算得![]() ,
,
所以有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】记
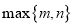 表示
表示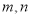 中的最大值,如
中的最大值,如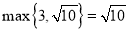 ,已知函数
,已知函数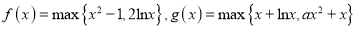 .
.(1)求函数
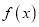 在
在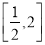 上的值域;
上的值域;(2)试探讨是否存在实数
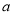 , 使得
, 使得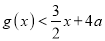 对
对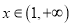 恒成立?若存在,求
恒成立?若存在,求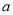 的取值范围;
的取值范围;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,如果集合AS,那么S的子集A的补集为SA={x|x∈S,且xA}.类似地,对于集合A、B,我们把集合{x|x∈A,且xB}叫作集合A与B的差集,记作A-B.据此回答下列问题:
(1)若A={1,2,3,4},B={3,4,5,6},求A-B;
(2)在下列各图中用阴影表示集合A-B.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在极坐标系中点C的极坐标为
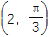 .
.(1)求出以点C为圆心,半径为2的圆的极坐标方程(写出解题过程)并画出图形;
(2)在直角坐标系中,以圆C所在极坐标系的极点为原点,极轴为x轴的正半轴建立直角坐标系,点P是圆C上任意一点,Q(5,-
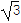 ),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程.
),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ∈[1,+∞).
∈[1,+∞).(1)当
 时,判断函数
时,判断函数 的单调性并证明;
的单调性并证明;(2)当
 时,求函数
时,求函数 的最小值;
的最小值;(3)若对任意
 ∈[1,+∞),
∈[1,+∞), >0恒成立,试求实数
>0恒成立,试求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
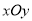 中,椭圆
中,椭圆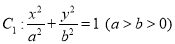 的左、右焦点分别为
的左、右焦点分别为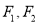 ,
, 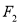 也是抛物线
也是抛物线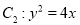 的焦点,点M为
的焦点,点M为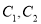 在第一象限的交点,且
在第一象限的交点,且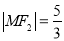 .
.(1)求
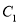 的方程;
的方程;(2)平面上的点N满足
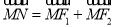 ,直线
,直线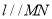 ,且与
,且与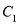 交于A,B两点,若
交于A,B两点,若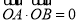 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程cos2x-sinx+a=0在(0,
 ]上有解,求a的取值范围.
]上有解,求a的取值范围.
相关试题

