【题目】已知{an}是等比数列,{bn}是等差数列,且a1=b1=1,a1+a2=b4 , b1+b2=a2 .
(1)求{an}与{bn}的通项公式;
(2)记数列{an+bn}的前n项和为Tn , 求Tn .
参考答案:
【答案】
(1)解:设等比数列{an}的公比为q,等差数列{bn}的公差为d,
由a1=b1=1得,an=1×qn﹣1,bn=1+(n﹣1)d,
由a1+a2=b4,b1+b2=a2得, ![]() ,
,
解得d=1,q=3,
所以an=3n﹣1,bn=n;
(2)解:由(1)得,an+bn=n+3n﹣1,
∴Tn=(1+30)+(2+32)+…+(n+3n﹣1)
=(1+2+…+n)+(30+32+…+3n﹣1)
= ![]() =
= ![]()
【解析】(1)设出公比和公差,根据等差、等比数列的通项公式,列出方程组求出公比和公差,再求出an、bn;(2)由(1)求出an+bn , 利用分组求和法、等比、等差数列的前n项和公式求出Tn .
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系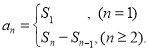 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
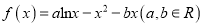 .
.(1)若
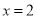 是函数
是函数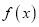 的一个极值点,
的一个极值点, 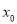 和1是
和1是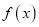 的两个零点,且
的两个零点,且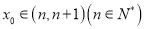 ,求
,求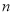 的值;
的值;(2)若
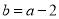 ,且
,且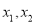 是
是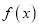 的两个极值点,求证:当
的两个极值点,求证:当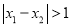 时,
时, 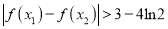 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若钝角三角形的三边长和面积都是整数,则称这样的三角形为“钝角整数三角形”,下列选项中能构成一个“钝角整数三角形”三边长的是( )
A.2,3,4
B.2,4,5
C.5,5,6
D.4,13,15 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的三视图如图所示(单位:cm),则该几何体的体积是cm3 , 该几何体的表面积是cm2 .
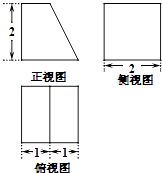
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x+t,g(x)=x2﹣t(t∈R)
(1)当x∈[2,3]时,求函数f(x)的值域(用t表示)
(2)设集合A={y|y=f(x),x∈[2,3]},B={y|y=|g(x)|,x∈[2,3]},是否存在正整数t,使得A∩B=A.若存在,请求出所有可能的t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若正项数列{an}满足:
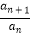 =an+1﹣an(a∈N*),则称此数列为“比差等数列”.
=an+1﹣an(a∈N*),则称此数列为“比差等数列”.
(1)请写出一个“比差等数列”的前3项的值;
(2)设数列{an}是一个“比差等数列”
(i)求证:a2≥4;
(ii)记数列{an}的前n项和为Sn , 求证:对于任意n∈N*,都有Sn>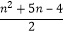 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD﹣A'B'C'D'中,点P在线段AD'上,且AP≤
 AD'则异面直线CP与BA'所成角θ的取值范围是 .
AD'则异面直线CP与BA'所成角θ的取值范围是 . 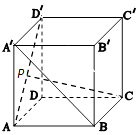
相关试题

