【题目】已知函数f(x)=x2﹣2x+t,g(x)=x2﹣t(t∈R)
(1)当x∈[2,3]时,求函数f(x)的值域(用t表示)
(2)设集合A={y|y=f(x),x∈[2,3]},B={y|y=|g(x)|,x∈[2,3]},是否存在正整数t,使得A∩B=A.若存在,请求出所有可能的t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵f(x)=(x﹣1)2+t﹣1,x∈[2,3],
对称轴x=1,f(x)在[2,3]递增,
∴x=2时,f(x)最小,f(2)=t,
x=3时,f(x)最大,f(3)=t+3,
∴f(x)的值域是[t,t+3];
(2)解:由(1)得:A=[t,t+3],B即为|g(x)|的值域,
∵A∩B=A,∴AB,
∵g(x)=x2﹣t,x∈[2,3],
假设存在正整数t符合要求,
①当1≤ ![]() ≤2时,即1≤t≤4时,
≤2时,即1≤t≤4时,
|g(x)|的值域是B=[4﹣t,9﹣t],
由4﹣t≤t<t+3≤9﹣t,
∴2≤t≤3,
∴t=2或3,
②当2< ![]() <3时,即4<t<9时:
<3时,即4<t<9时:
|g(x)|的值域B=[0,M],其中M=max{﹣f(2),f(3)}=max{t﹣4,9﹣t},
显然当4<t<9时,t+3>t﹣4且t+3>9﹣t,不符舍去,
③当 ![]() ≥3即t≥9时,
≥3即t≥9时,
|g(x)|的值域是B=[t﹣9,t﹣4],
由t﹣9≤t+3≤t﹣4,解集为空,
综上t=2或3.
【解析】(1)通过配方求出f(x)的值域;(2)求出集合A,通过讨论t的范围,求出集合B,解不等式求出t的值即可.
【考点精析】根据题目的已知条件,利用函数的值域和二次函数的性质的相关知识可以得到问题的答案,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若钝角三角形的三边长和面积都是整数,则称这样的三角形为“钝角整数三角形”,下列选项中能构成一个“钝角整数三角形”三边长的是( )
A.2,3,4
B.2,4,5
C.5,5,6
D.4,13,15 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的三视图如图所示(单位:cm),则该几何体的体积是cm3 , 该几何体的表面积是cm2 .
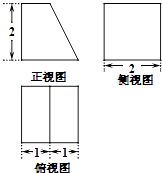
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等比数列,{bn}是等差数列,且a1=b1=1,a1+a2=b4 , b1+b2=a2 .
(1)求{an}与{bn}的通项公式;
(2)记数列{an+bn}的前n项和为Tn , 求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】若正项数列{an}满足:
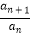 =an+1﹣an(a∈N*),则称此数列为“比差等数列”.
=an+1﹣an(a∈N*),则称此数列为“比差等数列”.
(1)请写出一个“比差等数列”的前3项的值;
(2)设数列{an}是一个“比差等数列”
(i)求证:a2≥4;
(ii)记数列{an}的前n项和为Sn , 求证:对于任意n∈N*,都有Sn>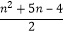 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD﹣A'B'C'D'中,点P在线段AD'上,且AP≤
 AD'则异面直线CP与BA'所成角θ的取值范围是 .
AD'则异面直线CP与BA'所成角θ的取值范围是 . 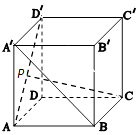
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点Pi(xi , yi)在直线li:aix+biy=ci上,若ai+bi=ici(i=1,2),且|P1P2|≥
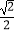 恒成立,则
恒成立,则  +
+  = .
= .
相关试题

