【题目】已知函数![]() .
.
(1)若![]() 是函数
是函数![]() 的一个极值点,
的一个极值点, ![]() 和1是
和1是![]() 的两个零点,且
的两个零点,且![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() 是
是![]() 的两个极值点,求证:当
的两个极值点,求证:当![]() 时,
时, ![]() .
.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)求导数![]() ,代入
,代入![]() ,1是
,1是![]() 的零点,所以
的零点,所以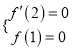 求出
求出![]() ,然后
,然后![]() 求得
求得![]() 在
在![]() 递增,在
递增,在![]() 递减,利用零点存在性确定
递减,利用零点存在性确定![]() ;(2)令
;(2)令![]() ,则
,则![]() ,令
,令![]() ,利用导数研究单调性,求其最小值.
,利用导数研究单调性,求其最小值.
试题解析:(1)由![]() ,得
,得![]() ,
,
因为![]() 是函数
是函数![]() 一个极值点,1是
一个极值点,1是![]() 的零点,所以
的零点,所以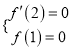 ,
,
即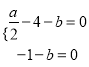 ,解得
,解得![]() ,
,
于是![]() ,
,
令![]() ,由
,由![]() ,解得
,解得![]() ,
,
则当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
于是![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
因为![]() 和1是
和1是![]() 的两个零点,且
的两个零点,且![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,则
,则![]() .
.
(2)由![]() ,得
,得![]() ,
,
则![]() ,
,
由![]() 是
是![]() 的两个极值点,得
的两个极值点,得![]() 是方程
是方程![]() 的两根1和
的两根1和![]() .
.
不妨令![]() ,则
,则![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,由
,由![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
于是当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 递增,在
递增,在![]() 递减.
递减.
于是![]() 在
在![]() 处取极小值
处取极小值![]() ,在
,在![]() 处取极大值
处取极大值![]() .
.
从而![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,则
,则![]() 递增,所以
递增,所以![]() ,
,
即![]() ,所以
,所以![]() 递增,
递增,
于是![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设α,β是两个不同的平面,m,n是两条不同的直线,有如下两个命题:q:若m⊥α,n⊥β且m∥n,则α∥β;q:若m∥α,n∥β且m∥n,则α∥β.( )
A.命题q,p都正确
B.命题p正确,命题q不正确
C.命题q,p都不正确
D.命题q不正确,命题p正确 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC是等腰三角形,BA=BC,DC⊥平面ABC,AE∥DC,若AC=2且BE⊥AD,则( )
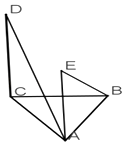
A.AB+BC有最大值
B.AB+BC有最小值
C.AE+DC有最大值
D.AE+DC有最小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O:x2+y2=1和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】若钝角三角形的三边长和面积都是整数,则称这样的三角形为“钝角整数三角形”,下列选项中能构成一个“钝角整数三角形”三边长的是( )
A.2,3,4
B.2,4,5
C.5,5,6
D.4,13,15 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的三视图如图所示(单位:cm),则该几何体的体积是cm3 , 该几何体的表面积是cm2 .
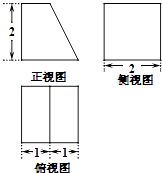
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等比数列,{bn}是等差数列,且a1=b1=1,a1+a2=b4 , b1+b2=a2 .
(1)求{an}与{bn}的通项公式;
(2)记数列{an+bn}的前n项和为Tn , 求Tn .
相关试题

