【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

参考答案:
【答案】②③.
【解析】分析:由题意结合所给的条件确定三角形解的个数即可确定是否能够唯一确定A,B两地之间的距离.
详解:考查所给的四个条件:
①测量∠A,AC,BC,已知两边及对角,由正弦定理可知,三角形有2个解,不能唯一确定点A,B两地之间的距离;
②测量∠A,∠B,BC,已知两角及一边,由余弦定理可知,三角形有唯一的解,能唯一确定点A,B两地之间的距离;
③测量∠C,AC,BC,已知两边及夹角,由余弦定理可知,三角形有唯一的解,能唯一确定点A,B两地之间的距离;
④测量∠A,∠C,∠B,知道三个角度值,三角形有无数多组解,不能唯一确定点A,B两地之间的距离;
综上可得,一定能唯一确定A,B两地之间的距离的所有方案的序号是②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意实数a,b,定义max{a,b}=
 , 已知在[﹣2,2]上的偶函数f(x)满足当0≤x≤2时,f(x)=max{2x﹣1,2﹣x}若方程f(x)﹣mx+1=0恰有两个根,则m的取值范围是( )
, 已知在[﹣2,2]上的偶函数f(x)满足当0≤x≤2时,f(x)=max{2x﹣1,2﹣x}若方程f(x)﹣mx+1=0恰有两个根,则m的取值范围是( )
A.[﹣2,﹣eln2)∪(eln2,2]
B.[﹣eln2,0)∪(0,eln2]
C.[﹣2,0)∪(0,2]
D.[﹣e,﹣2)∪(2,e] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆:
 , 左右焦点分别为F1 , F2 , 过F1的直线l交椭圆于A,B两点,若|BF2|+|AF2|的最大值为5,则b的值是
, 左右焦点分别为F1 , F2 , 过F1的直线l交椭圆于A,B两点,若|BF2|+|AF2|的最大值为5,则b的值是 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(2,5)和(8,3)是函数y=﹣k|x﹣a|+b与y=k|x﹣c|+d的图象仅有的两个交点,那么a+b+c+d的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=

 , g(x)=asin(
, g(x)=asin( x+
x+ π)﹣2a+2(a>0),给出下列结论:
π)﹣2a+2(a>0),给出下列结论:
①函数f(x)的值域为[0, ];
];
②函数g(x)在[0,1]上是增函数;
③对任意a>0,方程f(x)=g(x)在区间[0,1]内恒有解;
④若x1∈R,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是: ≤a≤
≤a≤ .
.
其中所有正确结论的序号为 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的外接圆半径
的外接圆半径 ,角A、B、C的对边分别是a、b、c,且
,角A、B、C的对边分别是a、b、c,且 .
. (I)求角B和边长b;
(II)求
 面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<
 )一个周期内的图象上的四个点,如图所示,A(﹣
)一个周期内的图象上的四个点,如图所示,A(﹣ , 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,
, 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称, 在x轴方向上的投影为
在x轴方向上的投影为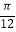 .
.
(1)求函数f(x)的解析式及单调递减区间;
(2)将函数f(x)的图象向左平移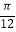 得到函数g(x)的图象,已知g(α)=
得到函数g(x)的图象,已知g(α)= , α∈(﹣
, α∈(﹣ , 0),求g(α+
, 0),求g(α+ )的值.
)的值.
相关试题

