【题目】已知点(2,5)和(8,3)是函数y=﹣k|x﹣a|+b与y=k|x﹣c|+d的图象仅有的两个交点,那么a+b+c+d的值为
参考答案:
【答案】18
【解析】解:∵函数y=﹣k|x﹣a|+b与y=k|x﹣c|+d的图象交于两点(2,5),(8,3),
∴5=﹣k|2﹣a|+b ①
3=﹣k|8﹣a|+b ②
5=k|2﹣c|+d ③
3=k|8﹣c|+d ④
①﹣②得2=﹣k|2﹣a|+k|8﹣a|⑤
③﹣④得2=k|2﹣c|﹣k|8﹣c|⑥
⑤=⑥得|8﹣a|+|8﹣c|=|2﹣c|+|2﹣a|
即|8﹣a|﹣|2﹣a|+|8﹣c|﹣|2﹣c|=0
设f(x)=|8﹣x|﹣|2﹣x|,则f(a)+f(c)=0,
画出函数f(x)的图象,如图,其关于点A(5,0)成中心对称,
故点a与点c关于点A(5,0)成中心对称,
∴![]() (a+c)=5,
(a+c)=5,
∴a+c=10,
又∵函数y=﹣k|x﹣a|+b的对称轴为x=a,函数y=k|x﹣c|+d的对称轴为x=c,
∴2<a<8,2<c<8
②+③:8=﹣k(8﹣a)+b+k(c﹣2)+d,
∴b+d=8,
∴a+b+c+d=18
故答案为:18.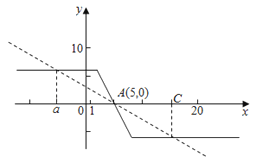
将两个交点代入函数y=﹣k|x﹣a|+b方程,得到方程组,将两个方程相减;据绝对值的意义及k的范围得到k,a满足的等式;同样的过程得到k,c满足的等式,两式联立求出a+c的值,再求出b+d,即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥S﹣ABC中,AB⊥BC,AB=BC=
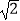 , SA=SC=2,二面角S﹣AC﹣B的余弦值是
, SA=SC=2,二面角S﹣AC﹣B的余弦值是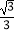 , 若S、A、B、C都在同一球面上,则该球的表面积是
, 若S、A、B、C都在同一球面上,则该球的表面积是 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
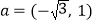 ,
,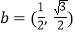 ,存在非零实数
,存在非零实数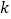 和
和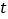 ,使得向量
,使得向量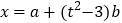 ,
,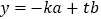 ,且
,且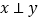 .问
.问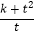 是否存在最小值?若存在,求其最小值;若不存在,说明理由.
是否存在最小值?若存在,求其最小值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
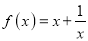 的图象为
的图象为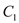 ,
, 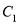 关于点
关于点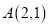 对称的图象为
对称的图象为 ,
, 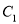 对应的函数为
对应的函数为 .
.(Ⅰ)求
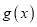 的解析式;
的解析式;(Ⅱ)若直线
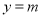 与
与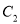 只有一个交点,求
只有一个交点,求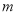 的值和交点坐标.
的值和交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是R上的奇函数,且
是R上的奇函数,且 的图象关于
的图象关于 对称,当
对称,当 时,
时,  ,
,(Ⅰ)当
 时,求
时,求 的解析式;
的解析式;(Ⅱ)计算
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是双曲线
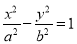 (a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
(a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且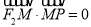 .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=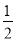 |NF1|=…=a。类似地:P是椭圆
|NF1|=…=a。类似地:P是椭圆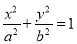 (a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
(a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且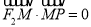 ,则|OM|的取值范围是________.
,则|OM|的取值范围是________.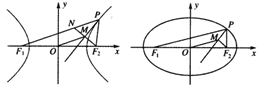
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 经过点
经过点 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形. (Ⅰ)求椭圆的方程;
(Ⅱ)若圆
 的任意一条切线
的任意一条切线 与椭圆E相交于P,Q两点,试问:
与椭圆E相交于P,Q两点,试问: 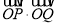 是否为定值? 若是,求这个定值;若不是,说明理由.
是否为定值? 若是,求这个定值;若不是,说明理由.
相关试题

