【题目】已知![]() 的外接圆半径
的外接圆半径![]() ,角A、B、C的对边分别是a、b、c,且
,角A、B、C的对边分别是a、b、c,且![]() .
.
(I)求角B和边长b;
(II)求![]() 面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
参考答案:
【答案】(Ⅰ)3;(Ⅱ)等边三角形.
【解析】试题分析:(Ⅰ)运用两角和的正弦公式将已知等式化简整理,得到![]() ,根据三角函数的诱导公式可得
,根据三角函数的诱导公式可得![]() ,从而得出
,从而得出![]() ,可得
,可得![]() ,最后由正弦定理可得
,最后由正弦定理可得![]() 的长;(Ⅱ)由
的长;(Ⅱ)由![]() 且
且![]() ,利用余弦定理算出
,利用余弦定理算出![]() ,再根据基本不等式算出
,再根据基本不等式算出![]() ,利用三角形的面积公式算出
,利用三角形的面积公式算出![]() ,从而得到当且仅当
,从而得到当且仅当![]() 时,
时, ![]() 有最大值
有最大值![]() ,进而得到此时
,进而得到此时![]() 是等边三角形.
是等边三角形.
试题解析:(Ⅰ) ![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]() ,
, ![]()
![]()
又![]() ,
,![]()
![]() ,
, ![]()
![]() ,即
,即![]()
又![]()
![]()
![]() ……4分
……4分
![]() 由正弦定理有:
由正弦定理有: ![]() ,于是
,于是![]()
(Ⅱ)由余弦定理![]() 得
得![]() ,
,![]()
![]()
![]()
![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取“=”
时取“=”
![]()
![]() ,即求
,即求![]() 面积的最大值为
面积的最大值为![]()
联立![]() ,解得
,解得![]()
又![]() ∴
∴![]() 为等边三角形.
为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点,
 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为 (
( 是参数),直线
是参数),直线 的极坐标方程为
的极坐标方程为 .
.(1)求直线
 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;(2)设点P为曲线C上任意一点,求点P到直线
 的距离的最大值.
的距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2+2x+a=0上存在两点关于直线l:mx+y+1=0对称. (Ⅰ)求m的值;
(Ⅱ)直线l与圆C交于A,B两点,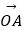
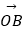 =﹣3(O为坐标原点),求圆C的方程.
=﹣3(O为坐标原点),求圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={x|a≤x≤2a﹣4},B={x|x2﹣5x﹣6<0},若A∩B=A,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中表示同一函数的是( )
A.y= 与y=(
与y=( 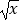 )4
)4
B.y=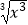 与y=
与y= 
C.y= ?与y=
?与y= 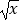 ?
? 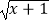
D.y= 与y=
与y= 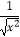
-
科目: 来源: 题型:
查看答案和解析>>【题目】正三棱柱
 的底边长为2,
的底边长为2, 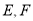 分别为
分别为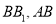 的中点.
的中点.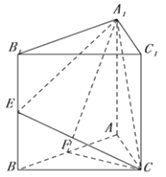
(1)已知
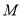 为线段
为线段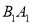 上的点,且
上的点,且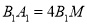 ,求证:
,求证: 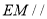 面
面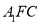 ;
;(2)若二面角
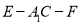 的余弦值为
的余弦值为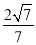 ,求
,求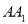 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a∈R,函数f(x)=
 +alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
+alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
(1)求a的值.
(2)如果函数y=f(x)和函数y=g(x)在区间(b,b+1)上均为增函数,求实数b的取值范围.
相关试题

