Question

【题目】对于任意实数a，b，定义max{a，b}= ， 已知在[﹣2，2]上的偶函数f（x）满足当0≤x≤2时，f（x）=max{2x﹣1，2﹣x}若方程f（x）﹣mx+1=0恰有两个根，则m的取值范围是（　　）
A.[﹣2，﹣eln2）∪（eln2，2]
B.[﹣eln2，0）∪（0，eln2]
C.[﹣2，0）∪（0，2]
D.[﹣e，﹣2）∪（2，e]

Answer 1

【答案】A
【解析】当1≤x≤2时，2x﹣1＞2﹣x，此时f（x）=2x﹣1，
当0≤x≤1时，2x﹣1＜2﹣x，此时f（x）=2﹣x，
即f（x）= ，
若﹣2≤x≤﹣1，则1≤﹣x≤2，此时f（﹣x）=2﹣x﹣1，
∵f（x）是偶函数，
∴f（x）=f（﹣x）=2﹣x﹣1，﹣2≤x≤﹣1．
若﹣1≤x≤0，则0≤﹣x≤1，此时f（﹣x）=2﹣x，
∵f（x）是偶函数，
∴f（x）=f（﹣x）=2﹣x，﹣1≤x≤0．
作出函数f（x）的图象如图：
由f（x）﹣mx+1=0得f（x）=mx﹣1，
设g（x）=mx﹣1，
则当m=0时，f（x）与g（x）没有交点，此时不满足条件．
当m＞0时，当x=1，f（1）=1，当x=2时，f（2）=3，
当直线经过A（1，1）时，此时m﹣1=1，则m=2，此时g（x）=2x﹣1，
g（2）=3，即直线g（x）=2x﹣1经过A，C点，此时两个曲线有两个交点，满足条件，
当直线y=mx﹣1与f（x）=2x﹣1相切时，
设切点为（k，n），
则f′（k）=2kln2，且2k﹣1=n，
则切线方程为y﹣n=2kln2（x﹣k），
即y=（2kln2）x﹣k2kln2+2k﹣1，
即2kln2=m，且﹣k2kln2+2k﹣1=﹣1，
即2kln2=m，且﹣k2kln2+2k=0，
2kln2=m，且﹣kln2+1=0，
即kln2=1，解得k==log2e，
则m==eln2，
此时直线和f（x）只有一个交点，
若时两个曲线有两个交点，则eln2＜m≤2，
根据偶函数的对称性知当m＜0时，﹣2≤m＜eln2，
综上m的取值范围是[﹣2，﹣eln2）∪（eln2，2]，
故选：A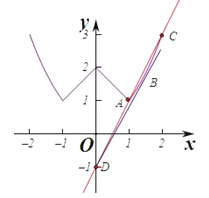

根据条件先求出当0≤x≤2时，函数f（x）的解析式，然后根据偶函数的性质求出函数在[﹣2，2]上解析式，利用函数与方程之间的关系转化为两个函数的相交问题，结合导数的几何意义求出切线斜率进行求解即可。