【题目】已知![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,
, ![]() ,
, ![]() 为函数
为函数![]() 的两个零点,求证:
的两个零点,求证: ![]() .
.
参考答案:
【答案】(Ⅰ)见解析; (Ⅱ)见解析.
【解析】试题分析: (Ⅰ)根据导数![]() ,分类讨论,当
,分类讨论,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, 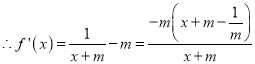 ,由
,由![]()
得![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,即可得出单调区间;(Ⅱ)由(Ⅰ)知
,即可得出单调区间;(Ⅱ)由(Ⅰ)知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .不妨设
.不妨设![]() ,由条件知
,由条件知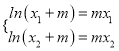 ,即
,即![]() ,构造函数
,构造函数![]() ,
, ![]() 与
与![]() 图像两交点的横坐标为
图像两交点的横坐标为![]() ,
, ![]() ,利用单调性只需证
,利用单调性只需证![]()
构造函数利用单调性证明.
试题解析:(Ⅰ) ![]() ,
, ![]()
当![]() 时,
时, ![]() ,即
,即![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间;
,无减区间;
当![]() 时,
时, 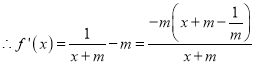 ,由
,由![]()
得![]()
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
![]() 时,易知
时,易知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(Ⅱ)由(Ⅰ)知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
不妨设![]() ,由条件知
,由条件知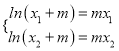 ,即
,即![]()
构造函数![]() ,
, ![]() 与
与![]() 图像两交点的横坐标为
图像两交点的横坐标为![]() ,
, ![]()
由![]() 可得
可得![]() ,
,
而![]() ,
, ![]()
知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
可知![]()
欲证![]() ,只需证
,只需证![]() ,即证
,即证![]()
考虑到![]() 在
在![]() 上递增,只需证
上递增,只需证![]()
由![]() 知,只需证
知,只需证![]()
令![]() ,
,
则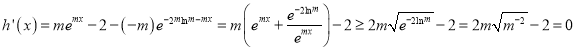
即![]() 单增,又
单增,又![]() ,
,
结合![]() 知
知![]() ,即
,即![]() 成立,
成立,
即![]() 成立
成立
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在区间(0,+∞)上的增函数,f(2)=1,且对于任意a,b∈(0,+∞),
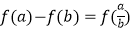 恒成立. (I)求f(8);
恒成立. (I)求f(8);
(II)求不等式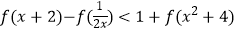 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且f(1)=2,f(2)=3. (I)若f(x)是偶函数,求出f(x)的解析式;
,且f(1)=2,f(2)=3. (I)若f(x)是偶函数,求出f(x)的解析式;
(II)若f(x)是奇函数,求出f(x)的解析式;
(III)在(II)的条件下,证明f(x)在区间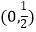 上单调递减.
上单调递减. -
科目: 来源: 题型:
查看答案和解析>>【题目】某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准如下:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知某学校学生的原始成绩均分布在[50,100]内,为了了解该校学生的成绩,抽取了50名学生的原始成绩作为样本进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出样本频率分布直方图如图所示.
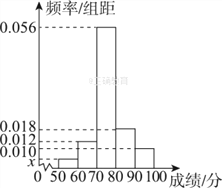
(Ⅰ)求图中x的值,并根据样本数据估计该校学生学业水平测试的合格率;
(Ⅱ)在选取的样本中,从70分以下的学生中随机抽取3名学生进行调研,用X表示所抽取的3名学生中成绩为D等级的人数,求随机变量X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0且a≠1,下列四组函数中表示相等函数的是( )
A.y=logax与y=(logxa)﹣1
B.y=2x与y=logaa2x
C.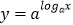 与y=x
与y=x
D.y=logax2与y=2logax -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为集合A,y=﹣x2+2x+2a的值域为B.
的定义域为集合A,y=﹣x2+2x+2a的值域为B.
(1)若a=2,求A∩B
(2)若A∪B=R,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=f(x)最大值为3,且f(﹣4)=f(0)=﹣1
(1)求f(x)的解析式;
(2)求f(x)在[﹣3,3]上的最值.
相关试题

