搜索
【题目】已知f（x）是定义在区间（0，+∞）上的增函数，f（2）=1，且对于任意a，b∈（0，+∞）， 
恒成立． （I）求f（8）；
（II）求不等式 
的解集．
参考答案：
【答案】解：（Ⅰ）令a=xy，b=y，则 
恒成立任意正数x，y都有f（xy）=f（x）+f（y）成立．由题意得，f（2）=1，任意正数x，y都有f（xy）=f（x）+f（y）成立，
令x1=x2=2，得f（4）=2f（2）=2，
令x1=4，x2=2，得f（8）=f（4）+f（2）=3；
（Ⅱ）不等式 
f（2x（x+2））＜f（2）+f（x2+4）f（2x2+4x）＜f（2x2+8）
解得0＜x＜2．故不等式解集为：（0，2）
【解析】（Ⅰ）利用条件、恒等式和赋值法即可求f（8）的值；（Ⅱ）由（Ⅰ）和恒等式将不等式等价转化为f（2x2+4x）＜f（2x2+8），结合函数的定义域、单调性列出不等式组，求解即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关，现从该市“五一”出游旅客中随机抽取500人进行调查，得到如下2×2列联表：（单位：人）
选择“有水的地方”
不选择“有水的地方”
合计
男
90
110
200
女
210
90
300
合计
300
200
500
（Ⅰ）据此样本，有多大的把握认为选择“有水的地方”与性别有关；
（Ⅱ）若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况，现从该市的全体出游旅客（人数众多）中随机抽取3人，设3人中选择“有水的地方”的人数为随机变量X，求随机变量X的数学期望和方差．
附临界值表及参考公式：
P（K2≥k0）
0.05
0.025
0.010
0.005
0.001
k0
3.841
5.024
6.635
7.879
10.828
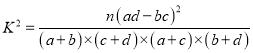，n＝a＋b＋c＋d． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知
，x∈R，且f（x）为奇函数． （I）求a的值及f（x）的解析式；
（II）判断函数f（x）的单调性． -
科目： 来源： 题型：
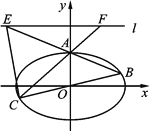
查看答案和解析>>【题目】如图，在平面直角坐标系
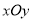中，椭圆： 
的离心率为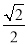
，直线l：y＝2上的点和椭圆上的点的距离的最小值为1．(Ⅰ) 求椭圆的方程；
(Ⅱ) 已知椭圆的上顶点为A，点B，C是上的不同于A的两点，且点B，C关于原点对称，直线AB，AC分别交直线l于点E，F．记直线
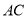与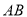
的斜率分别为
， 
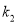．① 求证：
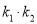为定值；② 求△CEF的面积的最小值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
，且f（1）=2，f（2）=3． （I）若f（x）是偶函数，求出f（x）的解析式；
（II）若f（x）是奇函数，求出f（x）的解析式；
（III）在（II）的条件下，证明f（x）在区间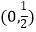
上单调递减． -
科目： 来源： 题型：
查看答案和解析>>【题目】某省2016年高中数学学业水平测试的原始成绩采用百分制，发布成绩使用等级制．各等级划分标准如下：85分及以上，记为A等；分数在[70，85）内，记为B等；分数在[60，70）内，记为C等；60分以下，记为D等．同时认定A，B，C为合格，D为不合格．已知某学校学生的原始成绩均分布在[50，100]内，为了了解该校学生的成绩，抽取了50名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出样本频率分布直方图如图所示．
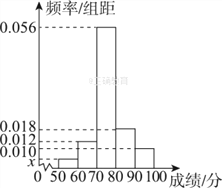
（Ⅰ）求图中x的值，并根据样本数据估计该校学生学业水平测试的合格率；
（Ⅱ）在选取的样本中，从70分以下的学生中随机抽取3名学生进行调研，用X表示所抽取的3名学生中成绩为D等级的人数，求随机变量X的分布列和数学期望．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
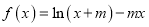.（Ⅰ）求
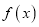的单调区间；（Ⅱ）设
， 
， 
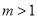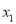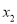为函数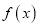
的两个零点，求证： 
.
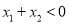相关试题
