【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处与直线
处与直线![]() 相切,求
相切,求![]() 的值;
的值;
(2)若函数![]() 有两个零点
有两个零点![]() ,试判断
,试判断![]() 的符号,并证明.
的符号,并证明.
参考答案:
【答案】(1) ![]() ;(2) 当
;(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
试题分析:(1)求函数![]() 的导数
的导数![]() ,由
,由![]() 可求
可求![]() 的值;(2)由(1)可知
的值;(2)由(1)可知![]() ,且定义域为
,且定义域为![]() ,先讨论当
,先讨论当![]() 时
时![]() 的零点是否符合题意,当
的零点是否符合题意,当![]() 时,由
时,由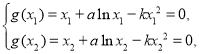 ,两式作差并整理得
,两式作差并整理得![]() ,则
,则![]() ,设
,设![]() ,
,![]() ,
,![]() ,,所以有
,,所以有![]() ,构造函数
,构造函数![]() ,讨论函数
,讨论函数![]() 的单调性与符号,可知
的单调性与符号,可知![]() 的符号.
的符号.
试题解析: (1)![]() ,又∵
,又∵![]() .………………2分
.………………2分
所以![]() .………………3分
.………………3分
(2)函数![]() 的定义域是
的定义域是![]() .………………4分
.………………4分
若![]() ,则
,则![]() .
.
令![]() ,则
,则![]() .
.
又据题设分析知![]() ,
,
∴![]() ,
,![]() .
.
又![]() 有两个零点,且都大于0,
有两个零点,且都大于0,
∴![]() ,不成立.………………5分
,不成立.………………5分
据题设知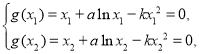
不妨设![]() ,
,![]() ,
,![]() .………………6分
.………………6分
所以![]() .
.
所以![]() .………………7分
.………………7分
又![]() ,
,
所以![]()
![]() .………………9分
.………………9分
引入![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递减.………………10分
上单调递减.………………10分
而![]() ,所以当
,所以当![]() 时,
时,![]() .
.
易知![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .………………12分
.………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 和
和 满足:
满足: ,
,
 ,
, ,其中
,其中 .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)记数列
 的前
的前 项和为
项和为 ,问是否存在正整数
,问是否存在正整数 ,使得
,使得 成立?若存在,求
成立?若存在,求 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
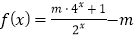 (
(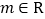 ).
).(1)若函数
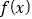 有零点,求实数
有零点,求实数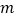 的取值范围;
的取值范围;(2)若对任意的
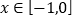 ,都有
,都有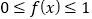 ,求实数
,求实数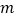 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗生长情况,从这批树苗中随机测量了其中50棵树苗的高度(单位:厘米),把这些高度列成了如下的频率分布表:
组别
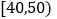
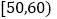

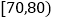
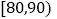
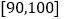
频数
2
3
14
15
12
4
(1)在这批树苗中任取一棵,其高度在85厘米以上的概率大约是多少?
(2)这批树苗的平均高度大约是多少?
(3)为了进一步获得研究资料,若从
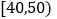 组中移出一棵树苗,从
组中移出一棵树苗,从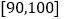 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则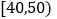 组中的树苗
组中的树苗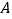 和
和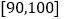 组中的树苗
组中的树苗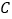 同时被移出的概率是多少?
同时被移出的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
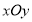 中,曲线
中,曲线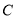 的参数方程为
的参数方程为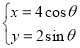 (
(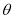 为参数).
为参数).(1)求曲线
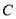 的普通方程;
的普通方程;(2)经过点
 (平面直角坐标系
(平面直角坐标系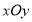 中点)作直线
中点)作直线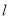 交曲线
交曲线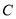 于
于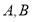 两点,若
两点,若 恰好为线段的三等分点,求直线
恰好为线段的三等分点,求直线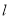 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
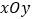 中,曲线
中,曲线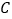 :
: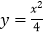 与直线
与直线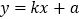 (
( )交于
)交于 ,
,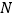 两点.
两点.(1)当
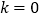 时,分别求
时,分别求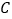 在点
在点 和
和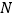 处的切线方程;
处的切线方程;(2)
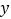 轴上是否存在点
轴上是否存在点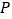 ,使得当
,使得当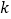 变动时,总有
变动时,总有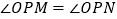 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
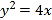 ,
,  是焦点,直线
是焦点,直线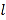 是经过点
是经过点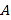 的任意直线.
的任意直线.(Ⅰ)若直线
 与抛物线交于
与抛物线交于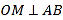 、
、 两点,且
两点,且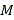 (
(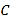 是坐标原点,
是坐标原点,  是垂足),求动点
是垂足),求动点 的轨迹方程;
的轨迹方程;(Ⅱ)若
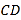 、
、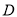 两点在抛物线
两点在抛物线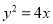 上,且满足
上,且满足 ,求证:直线
,求证:直线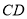 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标.
相关试题

