【题目】已知抛物线![]() ,
, ![]() 是焦点,直线
是焦点,直线![]() 是经过点
是经过点![]() 的任意直线.
的任意直线.
(Ⅰ)若直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且
两点,且![]() (
(![]() 是坐标原点,
是坐标原点, ![]() 是垂足),求动点
是垂足),求动点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若![]() 、
、![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,求证:直线
,求证:直线![]() 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标.
参考答案:
【答案】所求动点M的轨迹方程是![]() (
(![]() ).
).
直线CD的方程可化为![]() . 直线CD恒过定点,且定点坐标为(2,0).
. 直线CD恒过定点,且定点坐标为(2,0).
【解析】(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
解 (1) 设动点M的坐标为![]() . …………………1分
. …………………1分
∵抛物线![]() 的焦点是
的焦点是![]() ,直线l恒过点F,且与抛物线交于两点A、B,
,直线l恒过点F,且与抛物线交于两点A、B,
又![]() ,
,
∴![]() . …………………3分
. …………………3分
∴![]() ,化简,得
,化简,得![]() . …………………5分
. …………………5分
又当M与原点重合时,直线l与x轴重合,故![]() .
.
∴所求动点M的轨迹方程是![]() (
(![]() ).
).
(2) 设点C、D的坐标为![]() 、
、![]() . …………………………6分
. …………………………6分
∵C、D在抛物线![]() 上,
上,
∴![]() ,
, ![]() ,即
,即![]() ,
, ![]() .
.
又![]() ,
,
∴![]() . ………8分
. ………8分
∵点C、D的坐标为![]() 、
、![]() ,
,
∴直线CD的一个法向量是![]() ,可得直线CD的方程为:
,可得直线CD的方程为:
![]() ,化简,得
,化简,得
![]() ,进一步用
,进一步用![]() ,有
,有
![]() .
.
又抛物线![]() 上任两点的纵坐标都不相等,即
上任两点的纵坐标都不相等,即![]() .
.
∴直线CD的方程可化为![]() . ………………………10分
. ………………………10分
∴直线CD恒过定点,且定点坐标为(2,0). ………………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
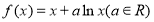 .
.(1)若曲线
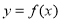 在点
在点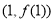 处与直线
处与直线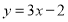 相切,求
相切,求 的值;
的值;(2)若函数
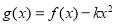 有两个零点
有两个零点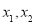 ,试判断
,试判断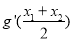 的符号,并证明.
的符号,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
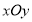 中,曲线
中,曲线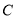 的参数方程为
的参数方程为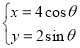 (
(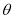 为参数).
为参数).(1)求曲线
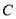 的普通方程;
的普通方程;(2)经过点
 (平面直角坐标系
(平面直角坐标系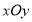 中点)作直线
中点)作直线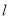 交曲线
交曲线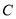 于
于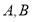 两点,若
两点,若 恰好为线段的三等分点,求直线
恰好为线段的三等分点,求直线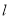 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
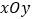 中,曲线
中,曲线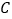 :
: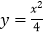 与直线
与直线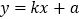 (
( )交于
)交于 ,
,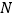 两点.
两点.(1)当
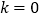 时,分别求
时,分别求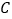 在点
在点 和
和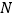 处的切线方程;
处的切线方程;(2)
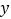 轴上是否存在点
轴上是否存在点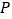 ,使得当
,使得当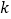 变动时,总有
变动时,总有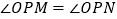 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
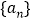 满足
满足 ,且
,且 ,
,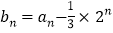 .
.(Ⅰ)求证:数列
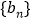 是等比数列;
是等比数列;(Ⅱ)设
 是数列
是数列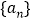 的前
的前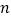 项和,若
项和,若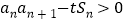 对任意的
对任意的 都成立,求实数
都成立,求实数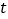 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中,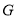 为
为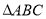 的重心,
的重心,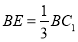 .
.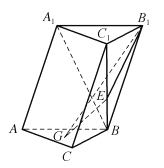
(1)求证:
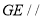 平面
平面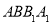 ;
;(2)若侧面
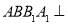 底面
底面 ,
,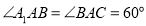 ,
, ,求直线
,求直线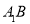 与平面
与平面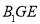 所成角
所成角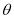 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
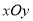 中,曲线
中,曲线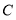 的参数方程为
的参数方程为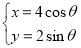 (
(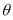 为参数).
为参数).(1)求曲线
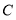 的普通方程;
的普通方程;(2)经过点
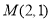 (平面直角坐标系
(平面直角坐标系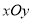 中点)作直线
中点)作直线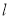 交曲线
交曲线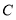 于
于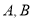 两点,若
两点,若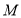 恰好为线段的三等分点,求直线
恰好为线段的三等分点,求直线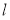 的斜率.
的斜率.
相关试题

