【题目】已知函数f(x)=  ,设a∈R,若关于x的不等式f(x)≥|
,设a∈R,若关于x的不等式f(x)≥| ![]() +a|在R上恒成立,则a的取值范围是( )
+a|在R上恒成立,则a的取值范围是( )
A.[﹣ ![]() ,2]
,2]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣2 ![]() ,2]
,2]
D.[﹣2 ![]() ,
, ![]() ]
]
参考答案:
【答案】A
【解析】解:当x≤1时,关于x的不等式f(x)≥| ![]() +a|在R上恒成立,
+a|在R上恒成立,
即为﹣x2+x﹣3≤ ![]() +a≤x2﹣x+3,
+a≤x2﹣x+3,
即有﹣x2+ ![]() x﹣3≤a≤x2﹣
x﹣3≤a≤x2﹣ ![]() x+3,
x+3,
由y=﹣x2+ ![]() x﹣3的对称轴为x=
x﹣3的对称轴为x= ![]() <1,可得x=
<1,可得x= ![]() 处取得最大值﹣
处取得最大值﹣ ![]() ;
;
由y=x2﹣ ![]() x+3的对称轴为x=
x+3的对称轴为x= ![]() <1,可得x=
<1,可得x= ![]() 处取得最小值
处取得最小值 ![]() ,
,
则﹣ ![]() ≤a≤
≤a≤ ![]() ①
①
当x>1时,关于x的不等式f(x)≥| ![]() +a|在R上恒成立,
+a|在R上恒成立,
即为﹣(x+ ![]() )≤
)≤ ![]() +a≤x+
+a≤x+ ![]() ,
,
即有﹣( ![]() x+
x+ ![]() )≤a≤
)≤a≤ ![]() +
+ ![]() ,
,
由y=﹣( ![]() x+
x+ ![]() )≤﹣2
)≤﹣2 ![]() =﹣2
=﹣2 ![]() (当且仅当x=
(当且仅当x= ![]() >1)取得最大值﹣2
>1)取得最大值﹣2 ![]() ;
;
由y= ![]() x+
x+ ![]() ≥2
≥2 ![]() =2(当且仅当x=2>1)取得最小值2.
=2(当且仅当x=2>1)取得最小值2.
则﹣2 ![]() ≤a≤2②
≤a≤2②
由①②可得,﹣ ![]() ≤a≤2.
≤a≤2.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过点
经过点 ,且圆心在直线
,且圆心在直线 :
: 上.
上.(1)求圆
 的方程;
的方程;(2)过点
 的直线与圆
的直线与圆 交于
交于 两点,问在直线
两点,问在直线 上是否存在定点
上是否存在定点 ,使得
,使得 恒成立?若存在,请求出点
恒成立?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏
B.3盏
C.5盏
D.9盏 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点
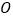 为极点,
为极点,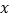 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线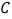 的极坐标方程为
的极坐标方程为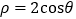 ,过点
,过点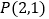 的直线
的直线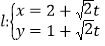 (
(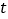 为参数)与曲线
为参数)与曲线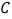 相交于
相交于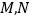 两点.
两点.(I)试写出曲线
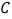 的直角坐标方程和直线
的直角坐标方程和直线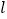 的普通方程;
的普通方程;(Ⅱ)求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20 , 接下来的两项是20 , 21 , 再接下来的三项是20 , 21 , 22 , 依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )
A.440
B.330
C.220
D.110 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3﹣x2=2.(12分)
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)如图,在平面直角坐标系xOy中,依次连接点P1(x1 , 1),P2(x2 , 2)…Pn+1(xn+1 , n+1)得到折线P1 P2…Pn+1 , 求由该折线与直线y=0,x=x1 , x=xn+1所围成的区域的面积Tn .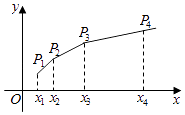
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}为等差数列,前n项和为Sn(n∈N+),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4﹣2a1 , S11=11b4 .
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nb2n﹣1}的前n项和(n∈N+).
相关试题

