【题目】已知圆![]() 经过点
经过点![]() ,且圆心在直线
,且圆心在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() 两点,问在直线
两点,问在直线![]() 上是否存在定点
上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,请求出点
恒成立?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)在直线
(2)在直线![]() 上存在定点
上存在定点![]() ,使得
,使得![]() 恒成立,详见解析
恒成立,详见解析
【解析】
(1)求出弦![]() 中垂线方程,由中垂线和直线
中垂线方程,由中垂线和直线![]() 相交得圆心坐标,再求出圆半径,从而得圆标准方程;
相交得圆心坐标,再求出圆半径,从而得圆标准方程;
(2)直线斜率存在时,设方程为![]() ,代入圆的方程,得
,代入圆的方程,得![]() 的一元二次方程,同时设交点为
的一元二次方程,同时设交点为![]() 由韦达定理得
由韦达定理得![]() ,假设定点存在,设其为
,假设定点存在,设其为![]() ,由
,由![]() 求得
求得![]() ,再验证所作直线斜率不存在时,
,再验证所作直线斜率不存在时,![]() 点也满足题意.
点也满足题意.
(1)![]() 的中点为
的中点为![]() ,∴
,∴![]() 的垂直平分线的斜率为
的垂直平分线的斜率为![]() ,
,
∴![]() 的垂直平分线的方程为
的垂直平分线的方程为![]() ,∴
,∴![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交点为圆心
交点为圆心![]() ,则
,则
![]() ,解得
,解得![]() ,
,
又![]() .
.
∴ 圆![]() 的方程为
的方程为![]() .
.
(2)当直线的斜率存在时,设直线的斜率为![]() ,则过点
,则过点![]() 的直线方程为
的直线方程为![]() ,故
,故
由![]() ,整理得
,整理得![]() ,
,
设![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
即![]()
![]() ,
,
当斜率不存在时,![]() 成立,
成立,
∴在直线![]() 上存在定点
上存在定点![]() ,使得
,使得![]() 恒成立
恒成立
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 的底面
的底面 是菱形,
是菱形, 底面
底面 ,
, 是
是 上的任意一点
上的任意一点
 求证:平面
求证:平面 平面
平面
 设
设 ,求点
,求点 到平面
到平面 的距离
的距离 在
在 的条件下,若
的条件下,若 ,求
,求 与平面
与平面 所成角的正切值
所成角的正切值 -
科目: 来源: 题型:
查看答案和解析>>【题目】
 两地相距
两地相距 千米,汽车从
千米,汽车从 地匀速行驶到
地匀速行驶到 地,速度不超过
地,速度不超过 千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度
千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度 的平方成正比,比例系数为
的平方成正比,比例系数为 ,固定部分为
,固定部分为 元,
元,(1)把全程运输成本
 (元)表示为速度
(元)表示为速度 (千米小时)的函效:并求出当
(千米小时)的函效:并求出当 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;(2)随着汽车的折旧,运输成本会发生一些变化,那么当
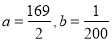 ,此时汽车的速度应调整为多大,才会使得运输成本最小,
,此时汽车的速度应调整为多大,才会使得运输成本最小, -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C与A,B两点,圆M是以线段AB为直径的圆.
(Ⅰ)证明:坐标原点O在圆M上;
(Ⅱ)设圆M过点P(4,﹣2),求直线l与圆M的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏
B.3盏
C.5盏
D.9盏 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点
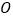 为极点,
为极点,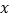 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线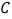 的极坐标方程为
的极坐标方程为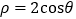 ,过点
,过点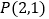 的直线
的直线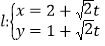 (
(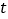 为参数)与曲线
为参数)与曲线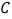 相交于
相交于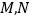 两点.
两点.(I)试写出曲线
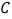 的直角坐标方程和直线
的直角坐标方程和直线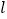 的普通方程;
的普通方程;(Ⅱ)求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,设a∈R,若关于x的不等式f(x)≥|
,设a∈R,若关于x的不等式f(x)≥|  +a|在R上恒成立,则a的取值范围是( )
+a|在R上恒成立,则a的取值范围是( )
A.[﹣ ,2]
,2]
B.[﹣ ,
,  ]
]
C.[﹣2 ,2]
,2]
D.[﹣2 ,
,  ]
]
相关试题

