【题目】通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
经计算![]() 的观测值
的观测值![]() . 参照附表,得到的正确结论是
. 参照附表,得到的正确结论是
附表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A. 有99%以上的把握认为“爱好该项运动与性别有关”
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
参考答案:
【答案】A
【解析】分析:直接将观测值![]() 和临界值表比对,即可得结果.
和临界值表比对,即可得结果.
详解:因为![]() ,
,
![]() 有
有![]() 以上的把握认为“爱好该项运动与性别有关”.
以上的把握认为“爱好该项运动与性别有关”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月14日.第一届“一带一路国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查,经统计“青少年”与“中老年” 的人数之比为9:11

(1)根据已知条件完成上面的列联表,并判断能否有99%的把握认为关注“一带一路”是和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查,在这9人中再取3人进打面对面询问,记选取的3人中“一带一路”的人数为X,求x的分布列及数学期望.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,若
中,若 ,
, ,
, 成等差数列,且三个内角
成等差数列,且三个内角 ,
, ,
, 也成等差数列,则
也成等差数列,则 的形状为__________.
的形状为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
,  为自然对数的底数).
为自然对数的底数).(Ⅰ)求函数
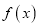 的极值;
的极值;(Ⅱ)当
 时,若直线
时,若直线 与曲线
与曲线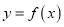 没有公共点,求
没有公共点,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从A1 , A2 , A3 , A4 , A5 , A6 , A7 , A8(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X.若X=0就参加学校合唱团,否则就参加学校排球队.

(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四位同学高考之后计划去
 三个不同社区进行帮扶活动,每人只能去一个社区,每个社区至少一人.其中甲必须去
三个不同社区进行帮扶活动,每人只能去一个社区,每个社区至少一人.其中甲必须去 社区,乙不去
社区,乙不去 社区,则不同的安排方法种数为 ( )
社区,则不同的安排方法种数为 ( )A. 24 B. 8 C. 7 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=
 ,连接CE并延长交AD于F
,连接CE并延长交AD于F 
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
相关试题

