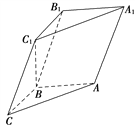
【题目】如图,在三棱柱ABCA1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=![]() .
.
(1)求证:C1B⊥平面ABC;
设![]() (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
试求λ的值.
参考答案:
【答案】(1)见解析(2)1
【解析】试题分析:(1)先由线面垂直的性质证明![]() ,再根据余玄定理及勾股定理证明
,再根据余玄定理及勾股定理证明![]() ,利用直线与平面垂直的判断定理证明
,利用直线与平面垂直的判断定理证明![]() 平面
平面![]() ;(2)通过
;(2)通过![]() 两两垂直.以
两两垂直.以![]() 为原点,
为原点,![]() 所在直线
所在直线![]() 轴建立空间直角坐标系.求出相关点的坐标,求出平面
轴建立空间直角坐标系.求出相关点的坐标,求出平面![]() 的一个法向量,平面BB1E的一个法向量,通过向量的数量积,推出
的一个法向量,平面BB1E的一个法向量,通过向量的数量积,推出![]() 的方程,求解即可.
的方程,求解即可.
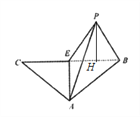
试题解析:(1)证明:因为AB⊥侧面BB1C1C,BC1侧面BB1C1C,故AB⊥BC1.
在△BCC1中,BC=1,CC1=BB1=2,∠BCC1=![]() ,
,
BC=BC2+CC-2BC·CC1·cos∠BCC1=12+22-2×1×2×cos![]() =3.
=3.
所以BC1=![]() ,故BC2+BC=CC,所以BC⊥BC1,
,故BC2+BC=CC,所以BC⊥BC1,
而BC∩AB=B 所以C1B⊥平面ABC.
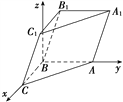
(2)由(1)可知,AB,BC,BC1两两垂直.以B为原点,BC,BA,BC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
则B(0,0,0),A(0,1,0),B1(-1,0,![]() ),C(1,0,0),C1(0,0,
),C(1,0,0),C1(0,0,![]() ).
).
所以=(-1,0,![]() ),所以=(-λ,0,
),所以=(-λ,0,![]() λ
λ![]() λ).
λ).
则=(1-λ,-1,![]() λ),=(-1,-1,
λ),=(-1,-1,![]() ).
).
设平面AB1E的法向量为n=(x,y,z),
则即![]()
令z=![]() ,则x=
,则x=![]() ,y=
,y=![]() ,
,
故n=![]() 是平面AB1E的一个法向量.
是平面AB1E的一个法向量.
因为AB⊥平面BB1C1C,所以=(0,1,0)是平面BB1E的一个法向量,
所以|cos〈n,〉|=
=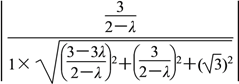
=![]() .
.
两边平方并化简得2λ2-5λ+3=0,所以λ=1或λ=![]() (舍去).
(舍去).
故所求λ的值为1
【方法点晴】本题主要考查线面垂直的判定定理以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
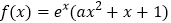 .
.(1)若
 ,求
,求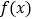 的单调区间;
的单调区间;(2)若函数
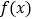 在
在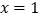 处有极值,请证明:对任意
处有极值,请证明:对任意 时,都有
时,都有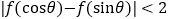 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
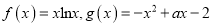
(Ⅰ)求函数
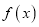 在
在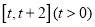 上的最小值;
上的最小值;(Ⅱ)设函数
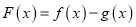 ,若函数
,若函数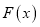 的零点有且只有一个,求实数
的零点有且只有一个,求实数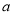 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.(1)求f(x)的解析式;
(2)k为何值时,方程f(x)-k=0只有1个根
(3)设函数g(x)=x2-2ax+a,若对于任意x1∈R,总存在x2∈[-1,0],使得g(x2)≤f(x1),求a的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照
 ,
,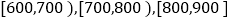 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.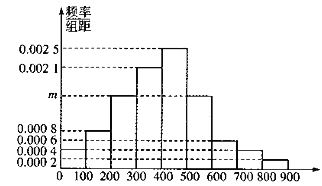
(1)求直方图中
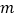 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用
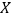 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量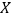 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市将建一个制药厂,但该厂投产后预计每天要排放大约80吨工业废气,这将造成极大的环境污染.为了保护环境,市政府决定支持该厂贷款引进废气处理设备来减少废气的排放,该设备可以将废气转化为某种化工产品和符合排放要求的气体,经测算,制药厂每天利用设备处理废气的综合成本
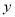 (元)与废气处理量
(元)与废气处理量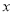 (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为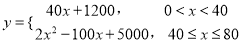 ,且每处理
,且每处理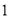 吨工业废气可得价值为
吨工业废气可得价值为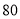 元的某种化工产品并将之利润全部用来补贴废气处理.
元的某种化工产品并将之利润全部用来补贴废气处理.(1)若该制药厂每天废气处理量计划定位20吨时,那么工厂需要每天投入的废气处理资金为多少元?
(2)若该制药厂每天废气处理量计划定为
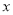 吨,且工厂不用投入废气处理资金就能完成计划的处理量,求
吨,且工厂不用投入废气处理资金就能完成计划的处理量,求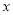 的取值范围;
的取值范围;(3)若该制药厂每天废气处理量计划定为
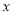 (
(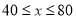 )吨,且市政府决定为处理每吨废气至少补贴制药厂
)吨,且市政府决定为处理每吨废气至少补贴制药厂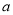 元以确保该厂完成计划的处理量总是不用投入废气处理资金,求
元以确保该厂完成计划的处理量总是不用投入废气处理资金,求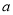 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券,赛后,中国男篮主力易建联荣膺本届亚锦赛
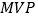 (最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.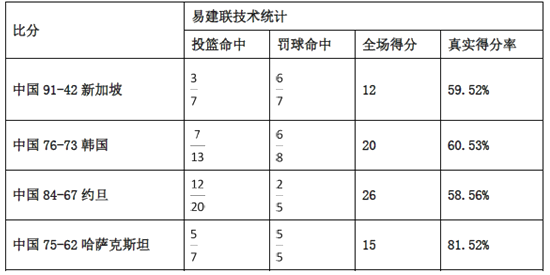
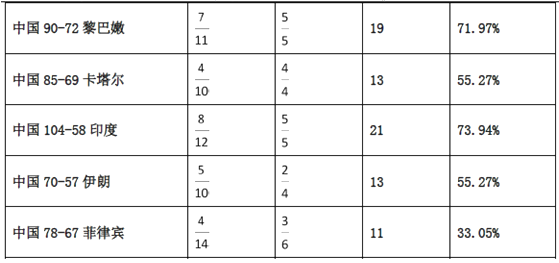
注:(1)表中
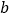 表示出手
表示出手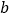 次命中
次命中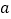 次;
次;(2)
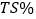 (真实得分率)是衡量球员进攻的效率,其计算公式为:
(真实得分率)是衡量球员进攻的效率,其计算公式为:
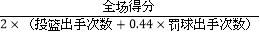
(1)从上述9场比赛中随机选择一场,求易建联在该场比赛中
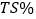 超过50%的概率;
超过50%的概率;(2)从上述9场比赛中随机选择一场,求易建联在该场比赛中
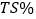 至少有一场超过60%的概率;
至少有一场超过60%的概率;(3)用
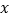 来表示易建联某场的得分,用
来表示易建联某场的得分,用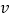 来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断
来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断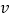 与
与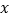 之间是否具有线性相关关系?结合实际简单说明理由.
之间是否具有线性相关关系?结合实际简单说明理由.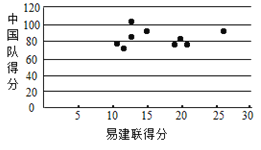
相关试题

