【题目】已知函数![]() (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.
(1)求f(x)的解析式;
(2)k为何值时,方程f(x)-k=0只有1个根
(3)设函数g(x)=x2-2ax+a,若对于任意x1∈R,总存在x2∈[-1,0],使得g(x2)≤f(x1),求a的取值范围
参考答案:
【答案】(1)![]() ;(2)k=
;(2)k=![]() 或0;(3)
或0;(3)![]() .
.
【解析】试题分析:(1)先由已知函数求其导数,再根据函数![]() 在
在![]() 处取得极值
处取得极值![]() ,列出关于
,列出关于![]() 的方程即可求得函数
的方程即可求得函数![]() 的解析式;(2)利用导数研究函数
的解析式;(2)利用导数研究函数![]() 的单调性,数形结合可得方程f(x)-k=0只有1个根时的
的单调性,数形结合可得方程f(x)-k=0只有1个根时的![]() 值;(3)函数g(x)=x2-2ax+a,若对于任意x1∈R,总存在x2∈[-1,0],使得g(x2)≤f(x1),等价于当
值;(3)函数g(x)=x2-2ax+a,若对于任意x1∈R,总存在x2∈[-1,0],使得g(x2)≤f(x1),等价于当![]() 时,
时, ![]()
![]() ,求出
,求出![]() ,结合换元法,分离参数后,利用基本不等式求解.
,结合换元法,分离参数后,利用基本不等式求解.
试题解析:(1)因为![]() ,所以
,所以![]() .
.
又f(x)在![]() 处取得极值2,所以
处取得极值2,所以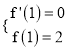 ,即
,即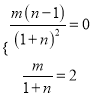 解得
解得![]() ,
,
经检验满足题意,所以![]() .
.
(2)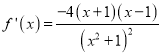 ,令
,令![]() ,得
,得![]() .
.
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:

所以f(x)在![]() 处取得极小值
处取得极小值![]() ,在
,在![]() 处取得极大值
处取得极大值![]() ,
,
又![]() 时,
时, ![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ,
,
![]() 如图
如图
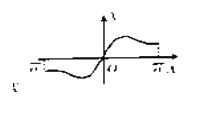
所以k=![]() 或0时,方程有一个根.
或0时,方程有一个根.
![]() (也可直接用方程来判断根的情况解决)
(也可直接用方程来判断根的情况解决)
(3)由(2)得![]() 的最小值为
的最小值为![]() ,
,
因为对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时, ![]() 有解,
有解,
即![]() 在
在![]() 上有解.
上有解.
令![]() ,则
,则![]() ,所以
,所以![]() .
.
所以当![]() 时,
时, ![]() ;
;
![]() 的取值范围为
的取值范围为![]() .
.
【方法点晴】本题主要考查不等式有解问题、方程根的个数问题以及函数极值问题,属于难题.不等式有解问题不能只局限于判别式是否为正,不但可以利用一元二次方程根的分布解题,还可以转化为![]() 有解(
有解(![]() 即可)或转化为
即可)或转化为![]() 有解(
有解(![]() 即可),本题(3)就用了这种方法.
即可),本题(3)就用了这种方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数f(x)=x
 (m∈N*).
(m∈N*).(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数还经过点(2,
 ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
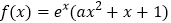 .
.(1)若
 ,求
,求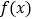 的单调区间;
的单调区间;(2)若函数
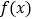 在
在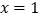 处有极值,请证明:对任意
处有极值,请证明:对任意 时,都有
时,都有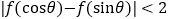 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
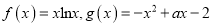
(Ⅰ)求函数
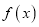 在
在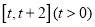 上的最小值;
上的最小值;(Ⅱ)设函数
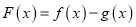 ,若函数
,若函数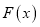 的零点有且只有一个,求实数
的零点有且只有一个,求实数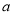 的值.
的值. -
科目: 来源: 题型:
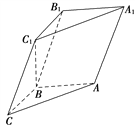
查看答案和解析>>【题目】如图,在三棱柱ABCA1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
 .
.(1)求证:C1B⊥平面ABC;
设
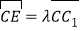 (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照
 ,
,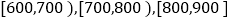 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.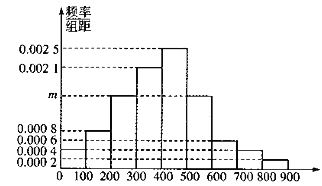
(1)求直方图中
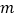 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用
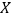 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量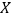 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市将建一个制药厂,但该厂投产后预计每天要排放大约80吨工业废气,这将造成极大的环境污染.为了保护环境,市政府决定支持该厂贷款引进废气处理设备来减少废气的排放,该设备可以将废气转化为某种化工产品和符合排放要求的气体,经测算,制药厂每天利用设备处理废气的综合成本
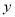 (元)与废气处理量
(元)与废气处理量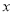 (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为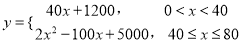 ,且每处理
,且每处理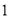 吨工业废气可得价值为
吨工业废气可得价值为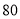 元的某种化工产品并将之利润全部用来补贴废气处理.
元的某种化工产品并将之利润全部用来补贴废气处理.(1)若该制药厂每天废气处理量计划定位20吨时,那么工厂需要每天投入的废气处理资金为多少元?
(2)若该制药厂每天废气处理量计划定为
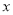 吨,且工厂不用投入废气处理资金就能完成计划的处理量,求
吨,且工厂不用投入废气处理资金就能完成计划的处理量,求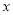 的取值范围;
的取值范围;(3)若该制药厂每天废气处理量计划定为
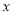 (
(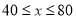 )吨,且市政府决定为处理每吨废气至少补贴制药厂
)吨,且市政府决定为处理每吨废气至少补贴制药厂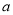 元以确保该厂完成计划的处理量总是不用投入废气处理资金,求
元以确保该厂完成计划的处理量总是不用投入废气处理资金,求 的值.
的值.
相关试题

