【题目】如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,所以CD⊥平面AOB,
因为∠BOP=60°,所以△OPB为正三角形,P到BO的距离为PE= ![]() ,E为BO的中点,AE=
,E为BO的中点,AE= ![]() =
= ![]() ,
,
AP= ![]() =
= ![]() ,
,
AP2=OP2+OA2﹣2OPOAcos∠AOP, ![]() ,
,
cos∠AOP= ![]() ,∠AOP=arccos
,∠AOP=arccos ![]() ,
,
A、P两点间的球面距离为 ![]() ,
,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中有大小、形状完全相同的四个小球,分别写有和、“谐”、“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生
 到
到 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用 ,
, ,
, ,
, 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下 组随机数:
组随机数:
由此可以估计,恰好第三次就停止摸球的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】智能手机的出现,改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从
 名手机使用者中随机抽取
名手机使用者中随机抽取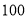 名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是:
名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是: 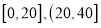 ,
, .
.
(1)根据频率分布直方图,估计这
 名手机使用者中使用时间的中位数是多少分钟? (精确到整数)
名手机使用者中使用时间的中位数是多少分钟? (精确到整数)(2)估计手机使用者平均每天使用手机多少分钟? (同一组中的数据以这组数据所在区间中点的值作代表)
(3)在抽取的
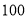 名手机使用者中在
名手机使用者中在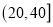 和
和 中按比例分别抽取
中按比例分别抽取 人和
人和 人组成研究小组,然后再从研究小组中选出
人组成研究小组,然后再从研究小组中选出 名组长.求这
名组长.求这 名组长分别选自
名组长分别选自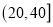 和
和 的概率是多少?
的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b为正实数.
(1)求证:
 ≥a+b;
≥a+b;(2)利用(1)的结论求函数y=
 (0<x<1)的最小值.
(0<x<1)的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某公司为郑州园博园生产某特许商品,该公司年固定成本为10万元,每生产千件需另投入2 .7万元,设该公司年内共生产该特许商品工x千件并全部销售完;每千件的销售收入为R(x)万元,
且
 ,
,(I)写出年利润W(万元〉关于该特许商品x(千件)的函数解析式;
〔II〕年产量为多少千件时,该公司在该特许商品的生产中所获年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
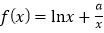 ,
, ,
, ,
, 为自然对数的底数.
为自然对数的底数.(Ⅰ)若函数
 在
在 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;(Ⅱ)若函数
 在
在 处的切线方程为
处的切线方程为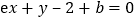 .求证:对任意的
.求证:对任意的 ,总有
,总有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某种书籍每册的成本费
 (元)与印刷册数
(元)与印刷册数 (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.






4.83
4.22
0.3775
60.17
0.60
-39.38
4.8

其中
 ,
, .
.为了预测印刷
 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型: ,
, .
.(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求
 关于
关于 的回归方程,并预测印刷
的回归方程,并预测印刷 千册时每册的成本费.
千册时每册的成本费.附:对于一组数据
 ,
, ,…,
,…, ,其回归方程
,其回归方程 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,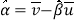 .
.
相关试题

