【题目】已知a,b为正实数.
(1)求证:![]() ≥a+b;
≥a+b;
(2)利用(1)的结论求函数y=![]() (0<x<1)的最小值.
(0<x<1)的最小值.
参考答案:
【答案】(1)见解析(2)1
【解析】
(1)证明:方法一:∵a>0,b>0,
∴(a+b)![]() =a2+b2+
=a2+b2+![]() ≥a2+b2+2ab=(a+b)2.
≥a2+b2+2ab=(a+b)2.
∴![]() ≥a+b,当且仅当a=b时等号成立.
≥a+b,当且仅当a=b时等号成立.
方法二:![]() -(a+b)
-(a+b)
![]() =
=![]() ,
,
又∵a>0,b>0,∴![]() ≥0,
≥0,
当且仅当a=b时等号成立.∴![]() ≥a+b.
≥a+b.
方法三:∵a>0,b>0,∴a2+b2≥2ab.
∴a+![]() ≥2b,b+
≥2b,b+![]() ≥2a,∴(a+b)+
≥2a,∴(a+b)+![]() ≥2a+2b.
≥2a+2b.
∴![]() ≥a+b.(当且仅当a=b时取等号).
≥a+b.(当且仅当a=b时取等号).
(2)∵0<x<1,∴1-x>0,
由(1)的结论,函数y=![]() ≥(1-x)+x=1.
≥(1-x)+x=1.
当且仅当1-x=x,即x=![]() 时等号成立.
时等号成立.
∴函数y=![]() (0<x<1)的最小值为1.
(0<x<1)的最小值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为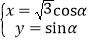 (其中
(其中 为参数),曲线
为参数),曲线 ,以坐标原点
,以坐标原点 为极点,以
为极点,以 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)求曲线
 的普通方程和曲线
的普通方程和曲线 的极坐标方程;
的极坐标方程;(2)若射线
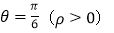 与曲线
与曲线 ,
, 分别交于
分别交于 两点,求
两点,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中有大小、形状完全相同的四个小球,分别写有和、“谐”、“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生
 到
到 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用 ,
, ,
, ,
, 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下 组随机数:
组随机数:
由此可以估计,恰好第三次就停止摸球的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】智能手机的出现,改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从
 名手机使用者中随机抽取
名手机使用者中随机抽取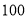 名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是:
名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是: 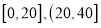 ,
, .
.
(1)根据频率分布直方图,估计这
 名手机使用者中使用时间的中位数是多少分钟? (精确到整数)
名手机使用者中使用时间的中位数是多少分钟? (精确到整数)(2)估计手机使用者平均每天使用手机多少分钟? (同一组中的数据以这组数据所在区间中点的值作代表)
(3)在抽取的
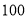 名手机使用者中在
名手机使用者中在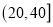 和
和 中按比例分别抽取
中按比例分别抽取 人和
人和 人组成研究小组,然后再从研究小组中选出
人组成研究小组,然后再从研究小组中选出 名组长.求这
名组长.求这 名组长分别选自
名组长分别选自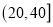 和
和 的概率是多少?
的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某公司为郑州园博园生产某特许商品,该公司年固定成本为10万元,每生产千件需另投入2 .7万元,设该公司年内共生产该特许商品工x千件并全部销售完;每千件的销售收入为R(x)万元,
且
 ,
,(I)写出年利润W(万元〉关于该特许商品x(千件)的函数解析式;
〔II〕年产量为多少千件时,该公司在该特许商品的生产中所获年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
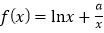 ,
, ,
, ,
, 为自然对数的底数.
为自然对数的底数.(Ⅰ)若函数
 在
在 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;(Ⅱ)若函数
 在
在 处的切线方程为
处的切线方程为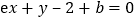 .求证:对任意的
.求证:对任意的 ,总有
,总有 .
.
相关试题

