【题目】已知函数![]() ,
,![]() ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若函数![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .求证:对任意的
.求证:对任意的![]() ,总有
,总有![]() .
.
参考答案:
【答案】(Ⅰ)![]() .
.
(Ⅱ)见解析.
【解析】分析:(Ⅰ)首先利用导数判断函数的单调性,然后由此求出函数的最小值,只要最小值小于0即可求出实数![]() 的取值范围;(Ⅱ)首先由条件得出
的取值范围;(Ⅱ)首先由条件得出![]() 的值确定函数解析式,然后由
的值确定函数解析式,然后由![]() 得到
得到![]() ,最后构造前后两个函数,验证前一个函数的最小值大于后一个函数的最大值。
,最后构造前后两个函数,验证前一个函数的最小值大于后一个函数的最大值。
详解:(Ⅰ)易得![]() .
.
若![]() ,有
,有![]() ,不合题意;
,不合题意;
若![]() ,有
,有![]() ,
,![]()
![]() ,满足题设;
,满足题设;
若![]() ,令
,令![]() ,得
,得![]()
∴![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 单调递增,
单调递增,
则![]() ,∴
,∴![]() .
.
又![]() 满足题设,
满足题设,
综上所述,所求实数![]() .
.
(Ⅱ)证明:易得,![]() ,
,
则由题意,得![]() ,解得
,解得![]() .
.
∴![]() ,从而
,从而![]() ,即切点为
,即切点为![]() .
.
将切点坐标代入![]() 中,解得
中,解得![]() . ∴
. ∴![]() .
.
要证![]() ,即证
,即证![]() (
(![]() ,
,
只需证![]()
![]() ).
).
令![]() ,
,![]()
![]() .
.
则由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增,
上单调递增,
∴![]() .
.
又由![]() ,得
,得![]()
∴![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减,
上单调递减,
∴![]() .
.
∴![]() ,
,
显然,上式的等号不能同时取到.
故对任意的![]() ,总有
,总有![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b为正实数.
(1)求证:
 ≥a+b;
≥a+b;(2)利用(1)的结论求函数y=
 (0<x<1)的最小值.
(0<x<1)的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某公司为郑州园博园生产某特许商品,该公司年固定成本为10万元,每生产千件需另投入2 .7万元,设该公司年内共生产该特许商品工x千件并全部销售完;每千件的销售收入为R(x)万元,
且
 ,
,(I)写出年利润W(万元〉关于该特许商品x(千件)的函数解析式;
〔II〕年产量为多少千件时,该公司在该特许商品的生产中所获年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某种书籍每册的成本费
 (元)与印刷册数
(元)与印刷册数 (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.






4.83
4.22
0.3775
60.17
0.60
-39.38
4.8

其中
 ,
, .
.为了预测印刷
 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型: ,
, .
.(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求
 关于
关于 的回归方程,并预测印刷
的回归方程,并预测印刷 千册时每册的成本费.
千册时每册的成本费.附:对于一组数据
 ,
, ,…,
,…, ,其回归方程
,其回归方程 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,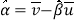 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级
 名学生中进行了抽样调查,发现喜欢甜品的占
名学生中进行了抽样调查,发现喜欢甜品的占 .这
.这 名学生中南方学生共
名学生中南方学生共 人。南方学生中有
人。南方学生中有 人不喜欢甜品.
人不喜欢甜品.(1)完成下列
 列联表:
列联表:喜欢甜品
不喜欢甜品
合计
南方学生
北方学生
合计
(2)根据表中数据,问是否有
 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;(3)已知在被调查的南方学生中有
 名数学系的学生,其中
名数学系的学生,其中 名不喜欢甜品;有
名不喜欢甜品;有 名物理系的学生,其中
名物理系的学生,其中 名不喜欢甜品.现从这两个系的学生中,各随机抽取
名不喜欢甜品.现从这两个系的学生中,各随机抽取 人,记抽出的
人,记抽出的 人中不喜欢甜品的人数为
人中不喜欢甜品的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:
 .
.
0.15
0.100
0.050
0.025
0.010

2.072
2.706
3.841
5.024
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的迅速发展,越来越多的消费者开始选择网络购物这种消费方式某营销部门统计了2019年某月锦州的十大特产的网络销售情况得到网民对不同特产的最满意度
 和对应的销售额
和对应的销售额 (万元)数据,如下表:
(万元)数据,如下表:特产种类
甲
乙
丙
丁
戊
已
庚
辛
壬
癸
最满意度











销售额
 (万元)
(万元)









 求销量额
求销量额 关于最满意度
关于最满意度 的相关系数
的相关系数 ;
; 我们约定:销量额
我们约定:销量额 关于最满意度
关于最满意度 的相关系数
的相关系数 的绝对值在
的绝对值在 以上(含
以上(含 )是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额
)是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额 关于最满意度
关于最满意度 的线性回归方程(系数精确到
的线性回归方程(系数精确到 ).
).参考数据:

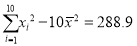 ,
,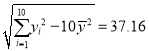 ,
, ,
, .
.附:对于一组数据
 .其回归直线方程
.其回归直线方程 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: ,
, .线性相关系数
.线性相关系数
相关试题

