搜索
【题目】袋子中有大小、形状完全相同的四个小球，分别写有和、“谐”、“校”“园”四个字，有放回地从中任意摸出一个小球，直到“和”、“谐”两个字都摸到就停止摸球，用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生
到
之间取整数值的随机数，分别用，
，
，代表“和”、“谐”、“校”、“园”这四个字，以每三个随机数为一组，表示摸球三次的结果，经随机模拟产生了以下
组随机数：
由此可以估计，恰好第三次就停止摸球的概率为（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】C
【解析】
由题随机数的前两位1,2只能出现一个，第三位出现另外一个.依次判断每个随机数即可.
由题随机数的前两位1,2只能出现一个，第三位出现另外一个,∴满足条件的随机数为142,112,241,142，故恰好第三次就停止摸球的概率为
.
故选：C
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
，
，其中
是自然常数.(1)判断函数
在
内零点的个数，并说明理由；(2)
，
，使得不等式
成立，试求实数
的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列
的前
项和为
，且
，
.（1）求数列
的通项公式；（2）已知
，记
（
且
），是否存在这样的常数
，使得数列
是常数列，若存在，求出的值；若不存在，请说明理由；（3）若数列
，对于任意的正整数，均有
成立，求证：数列是等差数列. -
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系
中，曲线
的参数方程为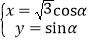
（其中
为参数），曲线
，以坐标原点
为极点，以
轴正半轴为极轴建立极坐标系.(1)求曲线
的普通方程和曲线
的极坐标方程；(2)若射线
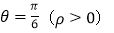与曲线，分别交于
两点，求
. -
科目： 来源： 题型：
查看答案和解析>>【题目】智能手机的出现，改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从
名手机使用者中随机抽取
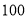名，得到每天使用手机时间(单位：分钟)的频率分布直方图(如图所示),其分组是: 
，
.
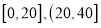（1）根据频率分布直方图，估计这
名手机使用者中使用时间的中位数是多少分钟? (精确到整数)（2）估计手机使用者平均每天使用手机多少分钟? (同一组中的数据以这组数据所在区间中点的值作代表)
（3）在抽取的
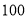名手机使用者中在
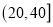和
中按比例分别抽取
人和
人组成研究小组，然后再从研究小组中选出名组长.求这名组长分别选自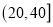和的概率是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b为正实数．
(1)求证：
≥a＋b；(2)利用(1)的结论求函数y＝
(0<x<1)的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，半径为R的半球O的底面圆O在平面α内，过点O作平面α的垂线交半球面于点A，过圆O的直径CD作平面α成45°角的平面与半球面相交，所得交线上到平面α的距离最大的点为B，该交线上的一点P满足∠BOP=60°，则A、P两点间的球面距离为（ ）
A.
B.
C.
D.
相关试题
