【题目】在平面直角坐标系中,已知![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求动点![]() 的轨迹方程,并说明曲线
的轨迹方程,并说明曲线![]() 是什么图形;
是什么图形;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)设![]() 是直线
是直线![]() 上的点,过
上的点,过![]() 点作曲线
点作曲线![]() 的切线
的切线![]() ,切点为
,切点为![]() ,设
,设![]() ,求证:过
,求证:过![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
参考答案:
【答案】(1)动点![]() 的轨迹方程为
的轨迹方程为![]() ,曲线
,曲线![]() 是以
是以![]() 为圆心,2为半径的圆(2)
为圆心,2为半径的圆(2)![]() 的方程为
的方程为![]() 或
或![]() .(3)证明见解析,所有定点的坐标为
.(3)证明见解析,所有定点的坐标为![]() ,
,![]()
【解析】
(1)利用两点间的距离公式并结合条件![]() ,化简得出曲线
,化简得出曲线![]() 的方程,根据曲线
的方程,根据曲线![]() 方程的表示形式确定曲线
方程的表示形式确定曲线![]() 的形状;
的形状;
(2)根据几何法计算出圆心到直线的距离![]() ,对直线
,对直线![]() 分两种情况讨论,一是斜率不存在,一是斜率存在,结合圆心到直线的距离
分两种情况讨论,一是斜率不存在,一是斜率存在,结合圆心到直线的距离![]() 求出直线的斜率,于此得出直线
求出直线的斜率,于此得出直线![]() 的方程;
的方程;
(3)设点![]() 的坐标为
的坐标为![]() ,根据切线的性质得出
,根据切线的性质得出![]() ,从而可得出过
,从而可得出过![]() 、
、![]() 、
、![]() 三点的圆的方程,整理得出
三点的圆的方程,整理得出![]() ,然后利用
,然后利用
 ,解出方程组可得出所过定点的坐标.
,解出方程组可得出所过定点的坐标.
(1)由题意得 ,化简可得:
,化简可得:![]() ,
,
所以动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
曲线![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆;
为半径的圆;
(2)①当直线![]() 斜率不存在时,
斜率不存在时,![]() ,不成立;
,不成立;
②当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,即
,即![]() ,
,
圆心![]() 到
到![]() 的距离为
的距离为![]() ∵
∵ ![]()
∴![]() , 即
, 即![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() 的方程为
的方程为![]() 或
或![]() ;
;
(3)证明:∵![]() 在直线
在直线![]() 上,则设
上,则设![]()
∵![]() 为曲线
为曲线![]() 的圆心,由圆的切线的性质可得
的圆心,由圆的切线的性质可得![]() ,
,
∴经过![]() 的三点的圆是以
的三点的圆是以![]() 为直径的圆,
为直径的圆,
则方程为![]() ,
,
整理可得![]() ,
,
令![]() ,且
,且![]() ,
,
解得![]() 或
或![]()
则有经过![]() 三点的圆必过定点,所有定点的坐标为
三点的圆必过定点,所有定点的坐标为![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,圆
中,圆 的参数方程为
的参数方程为 (
( 为参数).在极坐标系(与平面直角坐标系
为参数).在极坐标系(与平面直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线 的方程为
的方程为 .
.(Ⅰ)求圆
 的普通方程及直线
的普通方程及直线 的直角坐标方程;
的直角坐标方程;(Ⅱ)设平面直角坐标系
 中的点
中的点 ,经过点
,经过点 倾斜角为
倾斜角为 的直线
的直线 与
与 相交于
相交于 ,
, 两点,求
两点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 ﹣
﹣ 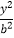 =1(a>0,b>0)的左焦点为F,离心率为
=1(a>0,b>0)的左焦点为F,离心率为  .若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
A.
=1
B.
=1
C.
=1
D.
=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,那么下列结论中错误的是( )
,那么下列结论中错误的是( )A. 若
 是
是 的极小值点,则
的极小值点,则 在区间
在区间 上单调递减
上单调递减B.
 ,使
,使
C. 函数
 的图像可以是中心对称图形
的图像可以是中心对称图形D. 若
 是
是 的极值点,则
的极值点,则
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1 , l2 , 直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )
A.16
B.14
C.12
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,且
,且 .
.(1)求
 的值及
的值及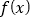 的定义域;
的定义域;(2)求
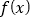 在区间
在区间 上的值域.
上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,双曲线
 =1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
=1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
相关试题

