【题目】如图,在三棱锥![]() 中,
中, ![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,
的中点, ![]() 平面
平面![]() ,
, ![]() ,二面角
,二面角![]() 为
为![]() .
.
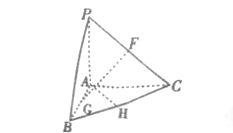
(1)证明: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据线面垂直的性质定理即可证明FG⊥AH;
(2)建立坐标系求出平面的法向量,利用向量法进行求解即可求二面角A-CP-B的余弦值.
试题解析:
(1)证明:如图,设![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() ,
,
![]()
![]() 为
为![]() 的中点,
的中点, ![]() .
.
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() .
.

(2)解: ![]() 平面
平面![]() ,
, ![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,以
,以![]() 为原点,在平面
为原点,在平面![]() 内过点
内过点![]() 垂直于
垂直于![]() 的直线为
的直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在的直线为
所在的直线为![]() 轴,建立如图所示的直角坐标系.则
轴,建立如图所示的直角坐标系.则 .
.
则![]() ,显然平面
,显然平面![]() 的一个法向量
的一个法向量![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则 ,即
,即 ,
,
得![]() .
.
又 ,
,
又二面角![]() 的平面角为锐角,
的平面角为锐角, ![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
 .
.(Ⅰ)求
 的最小值及取得最小值时
的最小值及取得最小值时 的取值范围;
的取值范围;(Ⅱ)若集合
 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)对于任意实数x,不等式sin x+cos x>m恒成立,求实数m的取值范围;
(2)存在实数x,不等式sin x+cos x>m有解,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角
的角 所对的边份别为
所对的边份别为 ,且
,且
(1)求角
 的大小;
的大小;(2)若
 ,求
,求 的周长
的周长 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
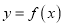 在实数集
在实数集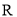 上的图象是连续不断的,且对任意实数
上的图象是连续不断的,且对任意实数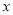 存在常数
存在常数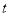 使得
使得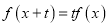 恒成立,则称
恒成立,则称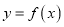 是一个“关于
是一个“关于 函数”.现有下列“关于
函数”.现有下列“关于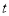 函数”的结论:
函数”的结论:①常数函数是“关于
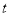 函数”;
函数”;②正比例函数必是一个“关于
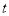 函数”;
函数”;③“关于
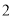 函数”至少有一个零点;
函数”至少有一个零点;④
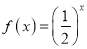 是一个“关于
是一个“关于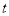 函数”.
函数”.其中正确结论的序号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD,

(Ⅰ)求证:平面PED⊥平面PAC;
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
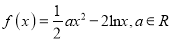 .
.(1)求函数
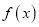 的单调区间;
的单调区间;(2)已知点
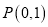 和函数
和函数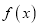 图像上动点
图像上动点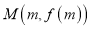 ,对任意
,对任意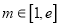 ,直线
,直线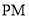 倾斜角都是钝角,求
倾斜角都是钝角,求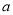 的取值范围.
的取值范围.
相关试题

