【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)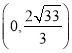
【解析】试题分析:(1)抛物线的焦点到准线的距离为![]() 可得
可得![]() ,从而得到抛物线的方程,然后设出切线切线
,从而得到抛物线的方程,然后设出切线切线![]() 的方程为
的方程为![]() ,由
,由![]() 求得
求得![]() ,由切点在抛物线上可得到
,由切点在抛物线上可得到![]() ,即为所求。(2)由(1)得到以线段
,即为所求。(2)由(1)得到以线段![]() 为直径的圆为圆
为直径的圆为圆![]() 。由题意只需考虑斜率为正数的直线
。由题意只需考虑斜率为正数的直线![]() 即可,根据几何知识得
即可,根据几何知识得![]() ,故
,故![]() 的方程为
的方程为![]() ,由弦长公式可得
,由弦长公式可得![]() ,又
,又![]() ,所以
,所以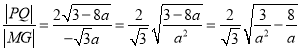 ,最后根据
,最后根据![]() 可得
可得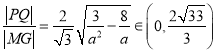 。
。
试题解析:
(1)由抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,得
,得![]() ,
,
则抛物线![]() 的方程为
的方程为![]() .
.
设切线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() ,
,
由![]() 得
得![]() ,
,
当![]() 时,点
时,点![]() 的横坐标为
的横坐标为![]() ,
,
则![]() ,
,
当![]() 时,同理可得
时,同理可得![]() .
.
综上得![]() 。
。
(2)由(1)知, ![]() ,
,
所以以线段![]() 为直径的圆为圆
为直径的圆为圆![]() ,
,
根据对称性,只要探讨斜率为正数的直线![]() 即可,
即可,
因为![]() 为直线
为直线![]() 与圆
与圆![]() 的切点,
的切点,
所以![]() ,
, ![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
由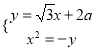 消去
消去![]() 整理得
整理得![]() ,
,
因为直线与圆相交,所以![]() 。
。
设![]() ,则
,则![]() ,
,
所以![]() ,
,
所以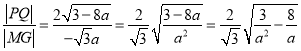 ,
,
设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以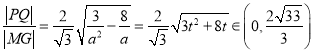 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 的一条弦被点
的一条弦被点 平分,则此弦所在的直线方程是( )
平分,则此弦所在的直线方程是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知椭圆
中,已知椭圆 的离心率为
的离心率为 ,且过点
,且过点 .
.(1)求
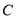 的方程;
的方程;(2)若动点
 在直线
在直线 上,过
上,过 作直线交椭圆
作直线交椭圆 于
于 两点,使得
两点,使得 ,再过
,再过 作直线
作直线 ,证明:直线
,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣1,其中n∈N* .
(1)求数列{an}的通项公式;
(2)设anbn= ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄的频数分布及支持“生育二胎”人数如表:
年龄
[5,15)
[15,25)
[25,35)
[35,45)
[45,55)
[55,65)
频数
5
10
15
10
5
5
支持“生育二胎”
4
5
12
8
2
1
(1)由以上统计数据填下面2乘2列联表,并问是否有的99%把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:
(2)若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望;年龄不低于45岁的人数
年龄低于45岁的人数
合计
支持
a=
c=
不支持
b=
d=
合计
参考数据:
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
K2=
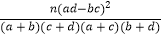 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 :实数
:实数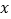 满足
满足 ,其中
,其中 ;
; :实数
:实数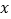 满足
满足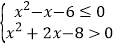 .
.(1)若
 ,且
,且 为真,
为真, 为假,求实数
为假,求实数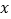 的取值范围;
的取值范围;(2)若
 是
是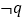 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
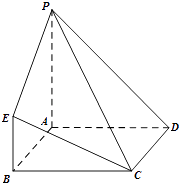
(1)求证:CE∥平面PAD;
(2)求PD与平面PCE所成角的正弦值;
(3)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
相关试题

