【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为![]() .设点
.设点![]() ,连接PA交椭圆于点C,坐标原点为O.
,连接PA交椭圆于点C,坐标原点为O.
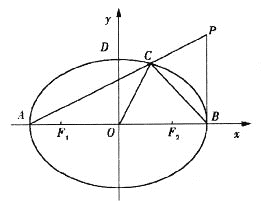
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求![]() 的最小值.
的最小值.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(I)由直线与圆相交,利用垂径定理列方程求解即可;
(Ⅱ)分别求得三角形ABC的面积和四边形OBPC的面积,由题意即可求得|t|的最小值.
试题解析:
(Ⅰ)因为以![]() 为直径的圆
为直径的圆![]() 过点
过点![]() ,所以
,所以![]() ,则圆
,则圆![]() 的方程为
的方程为![]() ,
,
又![]() ,所以
,所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与圆
与圆![]() 相交得到的弦长为
相交得到的弦长为![]() ,则
,则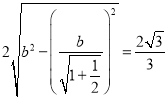 ,所以
,所以![]() ,
, ![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
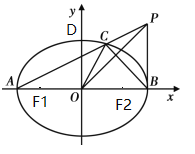
(Ⅱ)由已知得: ![]() ,
, ![]() ,椭圆方程为
,椭圆方程为![]() ,
,
设直线![]() 的方程为
的方程为![]() ,由
,由
整理得![]() ,
,
解得: ![]() ,
, ![]() ,则点
,则点![]() 的坐标是
的坐标是![]() ,
,
故直线![]() 的斜率为
的斜率为![]() ,由于直线
,由于直线![]() 的斜率为
的斜率为![]() ,
,
所以![]()
![]() ,所以
,所以![]() .
.
所以![]() ,
,
![]() ,所以
,所以![]() ,
,
整理得![]() ,
, ![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两集合A=[0,3],B=[0,3],分别从集合A、B中各任取一个元素m、n,即满足m∈A,n∈B,记为(m,n), (Ⅰ)若m∈Z,n∈Z,写出所有的(m,n)的取值情况,并求事件“方程
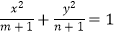 所对应的曲线表示焦点在x轴上的椭圆”的概率;
所对应的曲线表示焦点在x轴上的椭圆”的概率;
(Ⅱ)求事件“方程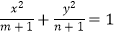 所对应的曲线表示焦点在x轴上的椭圆,且长轴长大于短轴长的
所对应的曲线表示焦点在x轴上的椭圆,且长轴长大于短轴长的 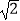 倍”的概率.
倍”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
 (其中e为自然对数的底数),
(其中e为自然对数的底数),  .
.(I)求函数
 的单调区间;
的单调区间;(II)设
 ,.已知直线
,.已知直线 是曲线
是曲线 的切线,且函数
的切线,且函数 上是增函数.
上是增函数.(i)求实数
 的值;
的值;(ii)求实数c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某省高考改革新方案,不分文理科,高考成绩实行“
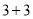 ”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体
”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体 ,从学生群体
,从学生群体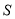 中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如下表:
中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如下表:
(I)从所调查的50名学生中任选2名,求他们选考物理、化学、生物科目数量不相等的概率;
(II)从所调查的50名学生中任选2名,记
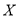 表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量
表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量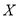 的分布列和数学期望;
的分布列和数学期望;(III)将频率视为概率,现从学生群体
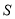 中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作
中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作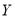 ,求事件“
,求事件“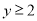 ”的概率.
”的概率. -
科目: 来源: 题型:
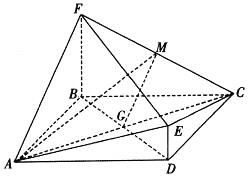
查看答案和解析>>【题目】如图,菱
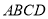 与四边形
与四边形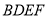 相交于
相交于 ,
, 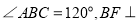 平面
平面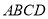 ,
, 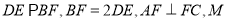 为
为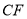 的中点,
的中点, 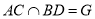 .
.
(I)求证:
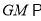 平面
平面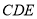 ;
; (II)求直线
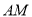 与平面
与平面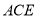 成角的正弦值.
成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:
①“等边三角形的三个内角均为60°”的逆命题;
②“若k>0,则方程x2+2x﹣k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题;
④“若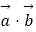 =
= 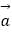
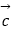 ,则
,则 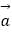 ⊥
⊥ 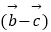 ”的否命题,
”的否命题,
其中真命题的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=a
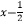 (a>0且a≠1),若f(lga)=
(a>0且a≠1),若f(lga)= 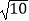 ,则a= .
,则a= .
相关试题

