【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求实数k的值;
(2)判断函数f(x)在(3,+∞)上的单调性,并利用定义证明;
(3)解关于x的不等式f(2x+6)>f(4x+3×2x+3).
参考答案:
【答案】(1)0;(2)详见解析;(3)(-∞,0).
【解析】
(1)根据f(x)是奇函数即可得出![]() ,从而可求出k=0;
,从而可求出k=0;
(2)先写出![]() ,根据单调性定义,设x1>x2>3,然后作差,通分,提取公因式,可判断出f(x1)>f(x2),从而得出f(x)在(3,+∞)上单调递增;
,根据单调性定义,设x1>x2>3,然后作差,通分,提取公因式,可判断出f(x1)>f(x2),从而得出f(x)在(3,+∞)上单调递增;
(3)根据上面得出的f(x)在(3,+∞)上是增函数,可由f(2x+6)>f(4x+3×2x+3)得出2x+6>4x+3×2x+3,解该不等式即可.
解:(1)f(x)是奇函数;
∴f(-x)=-f(x);
∴![]() ;
;
∴x2-kx+9=x2+kx+9;
∴-kx=kx;
∴k=0;
(2)![]() 在(3,+∞)上是增函数,证明如下:
在(3,+∞)上是增函数,证明如下:
设x1>x2>3,则:![]() =
=![]() ;
;
∵x1>x2>3;
∴x1-x2>0,x1x2>9,![]() ;
;
∴![]() ;
;
∴f(x1)-f(x2)>0;
∴f(x1)>f(x2);
∴f(x)在(3,+∞)上是增函数;
(3)由(2)知,f(x)在(3,+∞)上是增函数,且2x+6>3,4x+3×2x+3>3;
∴由f(2x+6)>f(4x+3×2x+3)得,2x+6>4x+3×2x+3;
∴(2x)2+2×2x-3<0;
∴-3<2x<1;
∴x<0;
∴原不等式的解集为(-∞,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】四棱柱
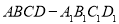 的底面ABCD为矩形,AB=1,AD=2,
的底面ABCD为矩形,AB=1,AD=2, ,
, ,则
,则 的长为( )
的长为( )A.
 B.
B.  C.
C. 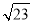 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的奇函数f(x),当x>0时,f(x)=ax2+bx+8(0<a<4),点A(2,0)在函数f(x)的图象上,且关于x的方程f(x)+1=0有两个相等的实根.
(1)求函数f(x)解析式;
(2)若x∈[t,t+2](t>0)时,函数f(x)有最小值1,求实数t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在公差不为零的等差数列{an}中,a2=1,a2、a4、a8成等比数列.
(1)求数列{an}的通项公式an;
(2)设数列{an}的前n项和为Sn , 记bn= .Tn=b1+b2+…+bn , 求Tn .
.Tn=b1+b2+…+bn , 求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤ω≤3,则居住满意度为二级;若0≤ω≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
人员编号
1
2
3
4
5
(x,y,z)
(1,1,2)
(2,1,1)
(2,2,2)
(0,1,1)
(1,2,1)
人员编号
6
7
8
9
10
(x,y,z)
(1,2,2)
(1,1,1)
(1,2,2)
(1,0,0)
(1,1,1)
(1)在这10名被调查者中任取两人,求这两人的居住满意度指标z相同的概率;
(2)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m﹣n,求随机变量ξ的分布列及其数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,已知
 ,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是
,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是 .则它们的大小关系是 (用“
.则它们的大小关系是 (用“ ”连接).
”连接). 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点,且
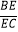 =λ.
=λ. 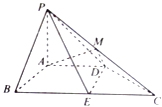
(1)求证:平面ADM⊥平面PBC;
(2)是否存在实数λ,使得二面角P﹣DE﹣B的余弦值为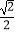 ?若存在,求出实数λ的值,若不存在,请说明理由.
?若存在,求出实数λ的值,若不存在,请说明理由.
相关试题

