搜索
【题目】四棱柱
的底面ABCD为矩形，AB＝1，AD＝2，
，
，则
的长为( )
A． 
B． 
C． 
D．
参考答案：
【答案】C
【解析】分析：记A1在面ABCD内的射影为O，O在∠BAD的平分线上，说明∠BAD的平分线即菱形ABCD的对角线AC，求AC1的长．
解答：解：记A1在面ABCD内的射影为O，
∵∠A1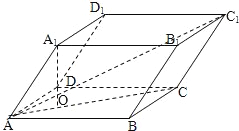
AB=∠A1AD，
∴O在∠BAD的平分线上，
由O向AB，AD两边作垂线，垂足分别为E，F，连接A1E，A1F，A1E，A1F分别垂直AB，AD于E，F
∵AA1=3，∠A1AB=∠A1AD=60°，
∴AE=AF=
又四棱柱ABCD-A1B1C1D1的底面ABCD为矩形
∴∠OAF=∠OAE=45°，且OE=OF=
，可得OA=
在直角三角形A1OA中，由勾股定理得A1O=
过C1作C1M垂直底面于M，则有△C1MC≌△A1OA，由此可得M到直线AD的距离是
，M到直线AB的距离是
，C1M=A1O=
所以AC1 =
=
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解关于x的不等式ax2-（2a+3）x+6＞0（a∈R）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在篮球比赛中，如果某位球员的得分，篮板，助攻，抢断，盖帽中有两个值达到
或
以上，就称该球员拿到了两双．下表是某球员在最近五场比赛中的数据统计：场次
得分
篮板
助攻
抢断
盖帽
（
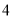
）从上述比赛中任选
场，求该球员拿到“两双”的概率．（
）从上述比赛中任选
场，设该球员拿到“两双”的次数为
，求
的分布列及数学期望．（
）假设各场比赛互相独立，将该球员在上述比赛中获得“两双”的频率作为概率，设其在接下来的三场比赛中获得“两双”的次数为
，试比赛
与
的大小关系（只需写出结论）． -
科目： 来源： 题型：
查看答案和解析>>【题目】某公司采用招考方式引进人才，规定必须在
，三个测试点中任意选取两个进行测试，若在这两个测试点都测试合格，则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点
测试合格的概率分别为
,小王在上述三个测试点测试合格的概率都是
.（1）问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大？请说明理由;
（2）假设小李选择测试点
进行测试，小王选择测试点
进行测试,记
为两人在各测试点测试合格的测试点个数之和,求随机变量
的分布列及数学期望
. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知定义域为R的奇函数f（x），当x＞0时，f（x）=ax2+bx+8（0＜a＜4），点A（2，0）在函数f（x）的图象上，且关于x的方程f（x）+1=0有两个相等的实根．
（1）求函数f（x）解析式；
（2）若x∈[t，t+2]（t＞0）时，函数f（x）有最小值1，求实数t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在公差不为零的等差数列{an}中，a2=1，a2、a4、a8成等比数列．
（1）求数列{an}的通项公式an；
（2）设数列{an}的前n项和为Sn ， 记bn=
．Tn=b1+b2+…+bn ， 求Tn ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
为奇函数．（1）求实数k的值；
（2）判断函数f（x）在（3，+∞）上的单调性，并利用定义证明；
（3）解关于x的不等式f（2x+6）＞f（4x+3×2x+3）．
相关试题
