【题目】如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,![]() ,
,![]() =4 ,
=4 ,![]() ,F为棱AE的中点.
,F为棱AE的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析,;(2)![]()
【解析】(1)如图,取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,因为
,因为![]() 为
为![]() 中点,所以
中点,所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .又
.又![]() 为正三角形,所以
为正三角形,所以
![]() ,从而
,从而![]() , (2分)
, (2分)
由![]() ,
,![]() ,可得
,可得![]() ,由平面ABC
,由平面ABC![]() 平面BCDE,平面ABC
平面BCDE,平面ABC![]() 平面BCDE=BC,
平面BCDE=BC,
可得![]() 平面ABC,因为
平面ABC,因为![]() 平面ABC,所以
平面ABC,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .(5分)
.(5分)
(2)因为![]() ,
,![]() ,所以
,所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 为
为![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() ,从而
,从而![]() .(7分)
.(7分)
以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
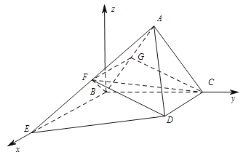
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,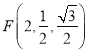 ,
,
所以![]() ,
,![]() .(8分)
.(8分)
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,即
,即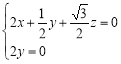 ,解得
,解得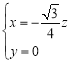 .
.
令![]() ,得
,得![]() .
.
由(1)可知![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
所以![]() .
.
因为二面角![]() 为钝角,所以其余弦值为
为钝角,所以其余弦值为![]() .(12分)
.(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
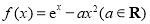 .
.(Ⅰ)若函数
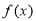 在
在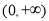 上单调递增,求实数
上单调递增,求实数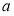 的取值范围;
的取值范围;(Ⅱ)若
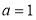 ,证明:
,证明: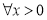 ,
,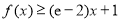 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
平面直角坐标系中,直线
 的参数方程为
的参数方程为 (
( 为参数),以原点为极点,
为参数),以原点为极点,  轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的极坐标方程与曲线
的极坐标方程与曲线 的直角坐标方程;
的直角坐标方程;(2)已知与直线
 平行的直线
平行的直线 过点
过点 ,且与曲线
,且与曲线 交于
交于 两点,试求
两点,试求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数y=f(x),当x≥0时,f(x)=x2﹣2x.
(1)求当x<0时,函数y=f(x)的解析式,并在给定坐标系下,画出函数y=f(x)的图象;
(2)写出函数y=|f(x)|的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
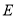 :
:  与圆
与圆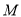 :
: 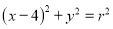 (
( )相交于
)相交于 、
、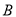 、
、 、
、 四个点.
四个点.(Ⅰ)求
 的取值范围;
的取值范围;(Ⅱ)当四边形
 的面积最大时,求对角线
的面积最大时,求对角线 、
、 的交点
的交点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)试判断f (x)的单调性,并证明你的结论;
(2)若f (x)为定义域上的奇函数,求函数f (x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:已知函数f(x)在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数f(x)在[m,n](m<n)上具有“DK”性质.例如函数
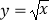 在[1,9]上就具有“DK”性质.
在[1,9]上就具有“DK”性质.
(1)判断函数f(x)=x2﹣2x+2在[1,2]上是否具有“DK”性质?说明理由;
(2)若g(x)=x2﹣ax+2在[a,a+1]上具有“DK”性质,求a的取值范围.
相关试题

