【题目】已知![]() .
.
(Ⅰ)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,证明:
,证明:![]() ,
,![]() 恒成立.
恒成立.
参考答案:
【答案】见解析
【解析】(Ⅰ)![]() .
.
由函数![]() 在
在![]() 上单调递增,可得
上单调递增,可得![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,得
,得![]() . -----------------2分
. -----------------2分
记![]() (
(![]() ),则
),则![]() .
.
当![]() 时,
时,![]() ,函数单调递减;当
,函数单调递减;当![]() 时,
时,![]() ,函数单调递增.
,函数单调递增.
所以![]() . -----------------5分
. -----------------5分
所以实数![]() 的取值范围为
的取值范围为![]() . ---------------------------6分
. ---------------------------6分
(Ⅱ)设![]() .
.
则![]() ,
,
记![]() ,则
,则![]() ,
,
故当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增. ------------9分
单调递增. ------------9分
又![]() ,
,![]() ,所以
,所以![]() ,使得
,使得![]() ,即
,即![]() .
.
所以当![]() 时,
时,![]() ,函数单调递增;
,函数单调递增;
当![]() 时,
时,![]() ,函数单调递减;
,函数单调递减;
当![]() 时,
时,![]() ,函数单调递增.
,函数单调递增.
而![]() ,
,
所以![]() 时,
时,![]() ,即
,即![]() 恒成立. -----------------13分
恒成立. -----------------13分
【命题意图】本题考查导数与函数的单调性、不等式的证明等,考查基本的逻辑推理能力、运算能力以及数学应用意识等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的4月23日是“世界读书日”,某校研究性学习小组为了解本校学生的阅读情况,随机调查了本校200名学生在这一天的阅读时间
 (单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
(单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.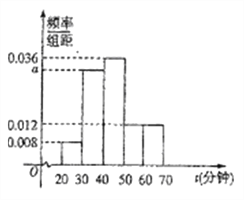
(1)求
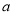 的值;
的值;(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这200名学生中,抽出25人参加交流会,则阅读时间为
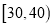 ,
, 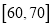 的两组中各抽取多少人?
的两组中各抽取多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行节日促销活动,消费满一定数额即可获得一次抽奖机会,抽奖这可以从以下两种方式中任选一种进行抽奖.
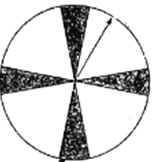
抽奖方式①:让抽奖者随意转动如图所示的圆盘,圆盘停止后指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为
 ,边界忽略不计)即中奖.
,边界忽略不计)即中奖.抽奖方式②:让抽奖者从装有3个白球和3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即中奖.
假如你是抽奖者,为了让中奖的可能性大,你应该选择哪一种抽奖方式?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中国人均读书4.3本(包括网络文学和教科书),比韩国的11本.法国的20本.日本的40本.犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用.出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国.礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天
 名读书者进行调查,将他们的年龄分成6段:
名读书者进行调查,将他们的年龄分成6段:  ,
,  ,
,  ,
,  ,
,  ,
,  后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:(1)估计在40名读书者中年龄分布在
 的人数;
的人数;(2)求40名读书者年龄的平均数和中位数;
(3)若从年龄在
 的读书者中任取2名,求恰有1名读书者年龄在
的读书者中任取2名,求恰有1名读书者年龄在 的概率.
的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
平面直角坐标系中,直线
 的参数方程为
的参数方程为 (
( 为参数),以原点为极点,
为参数),以原点为极点,  轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的极坐标方程与曲线
的极坐标方程与曲线 的直角坐标方程;
的直角坐标方程;(2)已知与直线
 平行的直线
平行的直线 过点
过点 ,且与曲线
,且与曲线 交于
交于 两点,试求
两点,试求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数y=f(x),当x≥0时,f(x)=x2﹣2x.
(1)求当x<0时,函数y=f(x)的解析式,并在给定坐标系下,画出函数y=f(x)的图象;
(2)写出函数y=|f(x)|的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,
 ,
, =4 ,
=4 , ,F为棱AE的中点.
,F为棱AE的中点.
(1)求证:平面
 平面
平面 ;
;(2)若直线
 与平面
与平面 所成角为
所成角为 ,求二面角
,求二面角 的余弦值.
的余弦值.
相关试题

